2022年浙江省寧波市重點高中保送生數學全真試卷（一）

一、選擇題（每小題5分，共25分）

• 1．在數軸上，點A、B在原點O的兩側，分別表示數a、2，將點A向右平移3個單位長度，得到點C．若CO=2BO，則a的值為（　　）

  A．-1

  B．-7

  C．1或-7

  D．7或-1
  組卷：4872引用：12難度：0.5

  解析

• 2．從1、2、3、4四個數中隨機選取兩個不同的數，分別記為a,c,則二次函數y=ax²+4x+c與x軸有兩個不同交點的概率為（　　）

  A． 1 4

  B． 1 3

  C． 1 2

  D． 2 3
  組卷：501引用：4難度：0.5

  解析

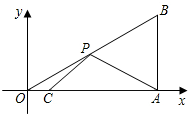• 3．如圖，在平面直角坐標系中，Rt△OAB的頂點A在x軸的正半軸上．頂點B的坐標為（3，

  3

  ），點C的坐標為（

  1

  2

  ，0），點P為斜邊OB上的一個動點，則PA+PC的最小值為（　　）

  A． 13 2

  B． 31 2

  C． 3 + 19 2

  D．2 7
  組卷：4789引用：65難度：0.7

  解析

三.解答題（共30分）

• 10．如圖，扇形OMN的半徑為1，圓心角是90°．點B是

  ?

  MN

  上一動點，BA⊥OM于點A，BC⊥ON于點C，點D、E、F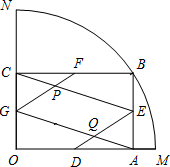、G分別是線段OA、AB、BC、CO的中點，GF與CE相交于點P，DE與AG相交于點Q．
  （1）求證：四邊形EPGQ是平行四邊形；
  （2）探索當OA的長為何值時，四邊形EPGQ是矩形；
  （3）連接PQ，試說明3PQ²+OA²是定值．
  組卷：1767引用：6難度：0.1

  解析

• 11．閱讀下列材料：
      我們知道，一次函數y=kx+b的圖象是一條直線，而y=kx+b經過恒等變形可化為直線的另一種表達形式：Ax+By+C=0（A、B、C是常數，且A、B不同時為0）．如圖1，點P（m,n）到直線l：Ax+By+C=0的距離（d）計算公式是：d=

  |

  A

  ×

  m

  +

  B

  ×

  n

  +

  C

  |

  A

  2

  +

  B

  2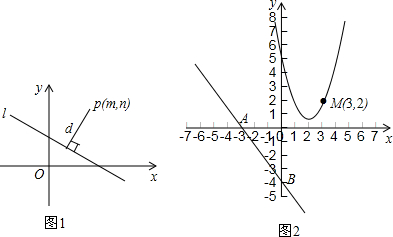

  ．
  
      例：求點P（1，2）到直線y=

  5

  12

  x-

  1

  6

  的距離d時，先將y=

  5

  12

  x

  -

  1

  6

  化為5x-12y-2=0，再由上述距離公式求得d=

  |

  5

  ×

  1

  +

  （

  -

  12

  ）

  ×

  2

  +

  （

  -

  2

  ）

  |

  5

  2

  +

  （

  -

  12

  ）

  2

  =

  21

  13

  ．
      解答下列問題：
      如圖2，已知直線y=-

  4

  3

  x

  -

  4

  與x軸交于點A，與y軸交于點B，拋物線y=x²-4x+5上的一點M（3，2）．
      （1）求點M到直線AB的距離．
      （2）拋物線上是否存在點P，使得△PAB的面積最小？若存在，求出點P的坐標及△PAB面積的最小值；若不存在，請說明理由．
  組卷：846引用：6難度：0.3

  解析