2022-2023學年黑龍江省雙鴨山市饒河高級中學高二（下）期末數學試卷

一、單選題共40分

• 1．設命題p：?x∈R，e^x=x+1，則p的否定為（　　）

  A．?x∈R，ex≠x+1	B．?x∈R，ex≠x+1
  C．?x?R，ex=x+1	D．?x?R，ex=x+1
  組卷：134引用：3難度：0.9

  解析

• 2．已知集合A={x|x²-2x=0}，B={x|x≤3，x∈N}，則A∩B=（　　）

  A．{2}

  B．{0，1，2，3}

  C．{1，2}

  D．{0，2}
  組卷：139引用：2難度：0.7

  解析

• 3．“a²+b²=2ab”是“a²=b²”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：216引用：4難度：0.7

  解析

• 4．函數

  f

  （

  x

  ）

  =

  2

  x

  x

  2

  +

  1

  的圖象大致為（　　）

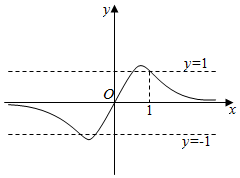
  A．	B．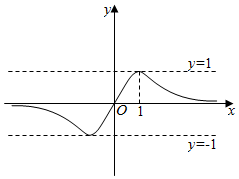
  C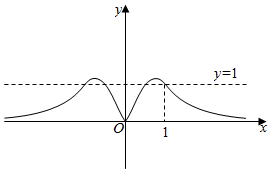．	D．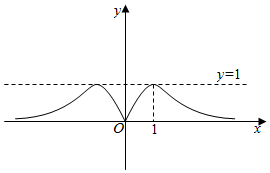
  組卷：127引用：16難度：0.8

  解析

• 5．已知

  f

  ′

  （

  x

  0

  ）

  =

  3

  ，

  lim

  Δ

  x

  →

  0

  f

  （

  x

  0

  +

  2

  Δ

  x

  ）

  -

  f

  （

  x

  0

  ）

  3

  Δ

  x

  的值是（　　）

  A．3

  B．1

  C．2

  D． 3 2
  組卷：84引用：5難度：0.8

  解析

• 6．已知函數f（x）=x（x-c）²在x=2處有極大值，則c的值為（　　）

  A．6

  B．6或2

  C．2

  D．4或2
  組卷：172引用：9難度：0.6

  解析

• 7．意大利畫家達?芬奇提出：固定項鏈的兩端，使其在重力的作用下自然下垂，那么項鏈所形成的曲線是什么？這就是著名的“懸鏈線問題”，其中雙曲余弦函數就是一種特殊的懸鏈線函數，其函數表達式為

  coshx

  =

  e

  x

  +

  e

  -

  x

  2

  ，相應的雙曲正弦函數的表達式為

  sinhx

  =

  e

  x

  -

  e

  -

  x

  2

  ．設函數

  f

  （

  x

  ）

  =

  sinhx

  coshx

  ，若實數a滿足不等式f（3a+20）+f（-2a²）＜0，則a的取值范圍為（　　）

  A． （ - 5 2 ， 4 ）	B． （ - 4 ， 5 2 ）
  C． （ - ∞ ，- 4 ） ∪ （ 5 2 ， + ∞ ）	D． （ - ∞ ，- 5 2 ） ∪ （ 4 ， + ∞ ）
  組卷：70引用：7難度：0.6

  解析

四、解答題共70分

• 21．已知橢圓E：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）過點（2，0），且左，右焦點分別為F₁（-

  3

  ，0），F₂（

  3

  ，0），直線y=kx與橢圓交于A，B兩點．
  （1）求橢圓E的方程；
  （2）若橢圓上一動點P（x,y），使得

  F

  1

  P

  ?

  F

  2

  P

  ＜0，求點P的橫坐標x的取值范圍．
  （3）設N（x,y）為橢圓上一點，且直線NA的斜率k₁∈（-2，-1），試求直線NB的斜率k₂的取值范圍．
  組卷：35引用：2難度：0.4

  解析

• 22．已知函數f（x）=

  1

  +

  2

  lnx

  x

  2

  ．
  （1）求f（x）的單調區間；
  （2）存在x₁，x₂∈（1，+∞）且x₁≠x₂，使|f（x₁）-f（x₂）|≥k|lnx₁-lnx₂|成立，求k的取值范圍．
  組卷：79引用：5難度：0.3

  解析