2022-2023學年山東省青島五十八中高一（上）期末數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符號選項要求的，線上誠信考試，請將選出的答案標號（A、B、C、D）使用小程序提交.

• 1．已知集合A={x|2^x＞4}，B={x|lnx＜1}，則集合A∩B=（　　）

  A．（-∞，e）

  B．（2，e）

  C．（-∞，1）

  D．（0，2）
  組卷：431引用：8難度：0.8

  解析

• 2．記cos（-80°）=k,那么tan100°=（　　）

  A． 1 - k 2 k

  B． - 1 - k 2 k

  C． k 1 - k 2

  D． - k 1 - k 2
  組卷：480引用：3難度：0.7

  解析

• 3．使不等式0＜

  1

  x

  ＜1成立的一個充分不必要條件是（　　）

  A．0＜x＜ 1 2

  B．x＞1

  C．x＞2

  D．x＜0
  組卷：770引用：9難度：0.7

  解析

• 4．已知函數f（x）=2^|x|，記

  a

  =

  f

  （

  （

  1

  4

  ）

  1

  3

  ）

  ，

  b

  =

  f

  （

  lo

  g

  3

  7

  2

  ）

  ，

  c

  =

  f

  （

  lo

  g

  1

  3

  5

  ）

  ，則a,b,c的大小關系為（　　）

  A．c＞b＞a

  B．b＞a＞c

  C．a＞b＞c

  D．c＞a＞b
  組卷：182引用：2難度：0.6

  解析

• 5．十六世紀中葉，英國數學家雷科德在《礪智石》一書中首先把“=”作為等號使用，后來英國數學家哈利奧特首次使用“＞”和“＜”符號，并逐步被數學界接受，不等號的引入對不等式的發展影響深遠．若實數

  x

  +

  3

  y

  =

  3

  （

  x

  ＞

  1

  ，

  y

  ＞

  1

  3

  ）

  ，則

  x

  x

  -

  1

  +

  3

  y

  3

  y

  -

  1

  的最小值為（　　）

  A．6

  B．4

  C．3

  D．2
  組卷：269引用：5難度：0.7

  解析

• 6．已知函數y=log_a（x-1）+1（a＞0且a≠1）恒過定點A（x₀，y₀），且滿足mx₀+ny₀=1，其中m,n是正實數，則

  2

  m

  +

  1

  n

  的最小值（　　）

  A．4

  B． 2 2

  C．9

  D． 2
  組卷：466引用：5難度：0.7

  解析

• 7．我國著名數學家華羅庚曾說：“數缺形時少直觀，形缺數時難入微，數形結合百般好，隔裂分家萬事休．”在數學的學習和研究中，常用函數的圖像來研究函數的性質，也常用函數的解析式來分析函數的圖像的特征，函數

  y

  =

  2

  x

  -

  2

  -

  x

  x

  3

  -

  x

  的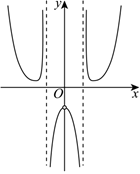圖像大致是（　　）

  A．

  B．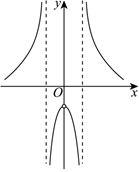

  C．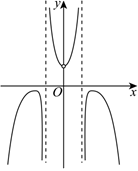

  D．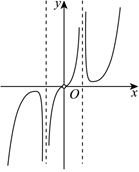
  組卷：241引用：7難度：0.6

  解析

四、解答題：本大題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.線上誠信考試，請將答案填寫在答題卡相應位置處，再拍照上傳.

• 21．已知函數f（x）=x²+2mx-6在區間[-1，2]上是單調函數．
  （1）求實數m的所有取值組成的集合A；
  （2）試寫出f（x）在區間[-1，2]上的最大值g（m）；
  （3）設h（x）=x+1，令F（m）=

  g （ m ） ， m ∈ A

  h （ m ） ， m ∈ ? RA

  ，若對任意

  m

  1

  ，

  m

  2

  ∈

  [

  -

  7

  2

  ，

  a

  ]

  ，總有|F（m₁）-F（m₂）|≤a+3，求a的取值范圍．
  組卷：67引用：2難度：0.5

  解析

• 22．截至2022年12月12日，全國新型冠狀病毒的感染人數突破44200000人．疫情嚴峻，請同學們利用的數學模型解決生活中的實際問題．
  【主題一】【科學抗疫，新藥研發】
  （1）我國某科研機構新研制了一種治療新冠肺炎的注射性新藥，并已進入二期臨床試驗階段．已知這種新藥在注射停止后的血藥含量c（t）（單位：mg/L）隨著時間t（單位：h）的變化用指數模型

  c

  （

  t

  ）

  =

  c

  0

  e

  -

  kt

  描述，假定某藥物的消除速率常數k=0.1（單位：h^-1），剛注射這種新藥后的初始血藥含量c₀=2000mg/L，且這種新藥在病人體內的血藥含量不低于1000mg/L時才會對新冠肺炎起療效，現給某新冠病人注射了這種新藥，則該新藥對病人有療效的時長大約為 _____（參考數據：ln2≈0.693，ln3≈1.099）
  A．5.32hB．6.23hC．6.93hD．7.52h
  【主題二】【及時隔離，避免感染】
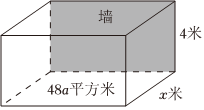
  （2）為了抗擊新冠，李滄區需要建造隔離房間．如圖，每個房間是長方體，且有一面靠墻，底面積為48a平方米（a＞0），側面長為x米，且x不超過8，房高為4米．房屋正面造價400元/平方米，側面造價150元/平方米．如果不計房屋背面、屋頂和地面費用，則側面長為多少時，總價最低．
  組卷：96引用：4難度：0.5

  解析