2014年4月全國100所名校單元測試示范卷數學（二）函數的概念及其性質（理科）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一個選項是符合題目要求的.

• 1．函數y=|x-1|+1的圖象的對稱軸方程為（　　）

  A．x=1

  B．x=-1

  C．y=1

  D．y=-1
  組卷：46引用：1難度：0.9

  解析

• 2．函數y=

  a

  2

  x

  （a≠0）的定義域為（　　）

  A．[0，+∞）	B．（0，+∞）
  C．{0}	D．以上答案都不對
  組卷：58引用：1難度：0.9

  解析

• 3．直角梯形ABCD如圖1，動點P從點B出發，由B→C→D→A沿邊運動，設點P運動的路程為x,△ABP的面積為f（x）．如果函數y=f（x）的圖象如圖2所示，則△ABC的面積為（　　）
  

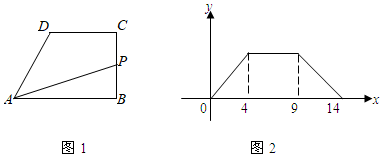
  A．10

  B．32

  C．18

  D．16
  組卷：64引用：23難度：0.9

  解析

• 4．已知函數f（x）=

  （ 2 - a ） x - 4 a , x ＜ 1

  ax , x ≥ 1

  是（-∞，+∞）上的增函數，則實數a的取值范圍是（　　）

  A．（0， 1 3 ）

  B．[ 1 3 ，2）

  C．（-1，0）

  D．（-1，2）
  組卷：393引用：2難度：0.9

  解析

• 5．若f_（x）=x²+ax+b-3，x∈R的圖象恒過（2，0），則a²+b²的最小值為（　　）

  A．5

  B．4

  C． 1 4

  D． 1 5
  組卷：82引用：10難度：0.7

  解析

• 6．已知函數f（x）=

  1 ， x ≥ 0

  - 1 ， x ＜ 0

  ，g（x）=x³，則f（x）?g（x）的奇偶性為（　　）

  A．是奇函數不是偶函數

  B．是偶函數不是奇函數

  C．是奇函數也是偶函數

  D．不是奇函數也不是偶函數
  組卷：176引用：3難度：0.7

  解析

• 7．已知圖甲為函數y=f（x）的圖象，則圖乙中的圖象對應的函數可能為（　　）

  A．y=|f（x）|

  B．y=f（|x|）

  C．y=f（-|x|）

  D．y=-f（-|x|）
  組卷：101引用：2難度：0.7

  解析

三、解答題：本大題共6小題，共70分.解答應寫出必要的文字說明、證明過程及演算步驟.

• 21．已知函數f（x）=

  a

  x

  2

  +

  1

  bx

  +

  c

  （a,c∈R，b∈N，a＞0，b＞0）是奇函數，在區間（0，+∞）上，函數有最小值2，且f（1）＜

  5

  2

  ．
  （1）求f（x）的解析式．
  （2）函數f（x）圖象上是否存在兩點關于點（1，0）對稱？若存在，求出這些點的坐標；若不存在，說明理由．
  組卷：67引用：2難度：0.1

  解析

• 22．對于定義域為D的函數y=f（x），若同時滿足：①f（x）在D內單調遞增或單調遞減；②存在區間[a,b]?D，使f（x）在[a,b]上的值域為[a,b]．那么把函數y=f（x）（x∈D）叫做“同族函數”．
  （1）求“同族函數”y=x²（x≥0）符合條件②的區間[a,b]．
  （2）是否存在實數k,使函數y=k+

  x

  +

  2

  是“同族函數”？若存在，求實數k的取值范圍；若不存在，請說明理由．
  組卷：61引用：2難度：0.5

  解析