2022-2023學年上海市普陀區(qū)宜川中學高二（下）期末數(shù)學試卷

一、填空題（本大題滿分54分）本大題共有12題。考生應在答題紙相應編號的空格內(nèi)直接填寫結果，1-6題每個空格填對得4分，7-12題每個空格填對得5分，否則一律得零分。

• 1．設集合A={1，3，5，7，9}，B={x|2≤x≤5}，則A∩B=

  ．
  組卷：370引用：3難度：0.9

  解析

• 2．不等式|x-1|≤2的解集為：

  ．（結果用集合或區(qū)間表示）
  組卷：341引用：7難度：0.7

  解析

• 3．已知直線l經(jīng)過點

  A

  （

  3

  ，

  3

  ）

  、

  B

  （

  3

  ，

  1

  ）

  ．直線l的傾斜角是

  ．
  組卷：124引用：3難度：0.7

  解析

• 4．已知

  π

  2

  ＜

  θ

  ＜

  π

  ，且

  cosθ

  =

  -

  4

  5

  ，則tan2θ=

  ．
  組卷：170引用：2難度：0.7

  解析

• 5．設隨機變量X服從正態(tài)分布N（2，σ²），若P（X≤1）=0.2，則P（X＜3）=

  ．
  組卷：334引用：8難度：0.8

  解析

• 6．某小組成員的年齡分布莖葉圖如圖所示，則該小組成員年齡的第25百分位數(shù)是

  ．
  組卷：182引用：8難度：0.9

  解析

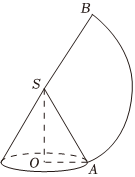• 7．如圖所示，圓錐SO的底面圓半徑OA=1，側面的平面展開圖的面積為3π，則此圓錐的體積為

  ．
  組卷：377引用：9難度：0.7

  解析

三、解答題（本大題滿分78分）本大題共有5題，解答下列各題必須在答題卷的相應編號規(guī)定區(qū)域內(nèi)寫出必要的步驟。

• 20．已知拋物線Γ：y²=4x.
  （1）求拋物線Γ的焦點F的坐標和準線l的方程；
  （2）過焦點F且斜率為

  1

  2

  的直線與拋物線Γ交于兩個不同的點A、B，求線段AB的長；
  （3）已知點P（1，2），是否存在定點Q，使得過點Q的直線與拋物線Γ交于兩個不同的點M、N（均不與點P重合），且以線段MN為直徑的圓恒過點P？若存在，求出點Q的坐標；若不存在，請說明理由．
  組卷：396引用：7難度：0.2

  解析

• 21．已知函數(shù)

  f

  （

  x

  ）

  =

  1

  2

  x

  2

  -

  （

  a

  +

  1

  ）

  x

  +

  alnx

  ．（其中a為常數(shù)）．
  （1）若a=-2，求曲線y=f（x）在點（2，f（2））處的切線方程；
  （2）當a＜0時，求函數(shù)y=f（x）的最小值；
  （3）當0≤a＜1時，試討論函數(shù)y=f（x）的零點個數(shù)，并說明理由．
  組卷：1190引用：7難度：0.9

  解析