2020-2021學(xué)年上海市浦東新區(qū)新場中學(xué)高二（下）周練數(shù)學(xué)試卷（11）

一、填空題：（每小題4分，共40分）

• 1．設(shè)A={正方體}，B={直平行六面體}，C={正四棱柱}，D={長方體}，那么上述四個集合間正確的包含關(guān)系是
  組卷：85引用：3難度：0.8

  解析

• 2．設(shè)F₁、F₂分別是雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）的左、右焦點，點P在雙曲線右支上且滿足|PF₂|=|F₁F₂|，雙曲線的漸近線方程為4x±3y=0，則cos∠PF₁F₂=

  ．
  組卷：464引用：5難度：0.6

  解析

• 3．已知點A、B到平面α的距離分別是4、6，則線段AB的中點M到平面的距離α是

  ．
  組卷：72引用：2難度：0.9

  解析

• 4．圓錐的側(cè)面積是底面積的3倍，若圓錐的母線長為3，則該圓錐的體積為

  ．（結(jié)果保留π）
  組卷：18引用：2難度：0.7

  解析

• 5．設(shè)P為曲線x²-4y²-4=0上一動點，O為坐標(biāo)原點，M為線段PO的中點，則點M的軌跡方程為

  ．
  組卷：462引用：3難度：0.7

  解析

三、解答題：（共3題=16+16+20）

• 14．已知拋物線C：y=2x²和直線l：y=kx+1，O為坐標(biāo)原點．
  （1）求證：l與C必有兩交點；
  （2）設(shè)l與C交于A，B兩點，且直線OA和OB斜率之和為1，求k的值．
  組卷：120引用：4難度：0.5

  解析

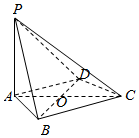• 15．如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．
  （1）求證：BD⊥平面PAC；
  （2）若PA=AB，求PB與AC所成角的余弦值；
  （3）當(dāng)平面PBC與平面PDC垂直時，求PA的長．
  組卷：454引用：7難度：0.5

  解析