2022-2023學年山東省泰安市新泰一中東校高二（下）第一次質檢數學試卷

一、單項選擇題（本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．設函數f（x）=lnx+1，則

  △

  x

  →

  0

  lim

  f

  （

  1

  +

  5

  △

  x

  ）

  -

  f

  （

  1

  ）

  △

  x

  =（　　）

  A．1

  B．5

  C． 1 5

  D．0
  組卷：267引用：5難度：0.8

  解析

• 2．設函數f（x）=cosx,則

  [

  f

  （

  π

  3

  ）

  ]

  ′

  =（　　）

  A． - 3 2

  B． 3 2

  C． 1 2

  D．0
  組卷：126引用：6難度：0.8

  解析

• 3．為了豐富學生的課余生活，某學校開設了籃球、書法、美術、吉他、舞蹈、擊劍共六門活動課程，甲、乙、丙3名同學從中各自任選一門活動課程參加，則這3名學生所選活動課程不全相同的選法有（　　）

  A．120種

  B．150種

  C．210種

  D．216種
  組卷：199引用：4難度：0.6

  解析

• 4．已知

  a

  =

  ln

  2

  2

  ，

  b

  =

  1

  e

  ，

  c

  =

  ln

  5

  5

  ，則以下不等式正確的是（　　）

  A．c＞b＞a

  B．a＞b＞c

  C．b＞a＞c

  D．b＞c＞a
  組卷：599引用：13難度：0.7

  解析

• 5．函數

  f

  （

  x

  ）

  =

  e

  x

  -

  1

  x

  的大致圖象為（　　）

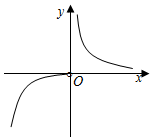
  A．	B．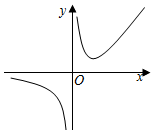
  C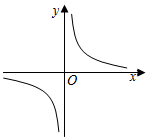．	D．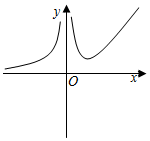
  組卷：213引用：21難度：0.7

  解析

• 6．由于新冠肺炎疫情，現有五名社區工作人員被分配到三個小區做社區監管工作，要求每人只能去一個小區，每個小區至少有一個人，則不同的分配方法有（　　）

  A．150種

  B．90種

  C．60種

  D．80種
  組卷：267引用：8難度：0.7

  解析

• 7．設函數

  f

  （

  x

  ）

  =

  2

  x

  -

  2

  x

  -

  alnx

  在（1，2）上單調遞減，則實數a的取值范圍是（　　）

  A．[4，5]

  B．（5，+∞）

  C．[4，+∞）

  D．[5，+∞）
  組卷：146引用：2難度：0.7

  解析

四、解答題（本大題共6小題，共70分.解答應寫出文字說明、證明過程或驗算步驟）

• 21．定義：

  C

  m

  x

  =

  x

  （

  x

  -

  1

  ）

  ?

  （

  x

  -

  m

  +

  1

  ）

  m

  !

  為廣義組合數，其中x∈R，m是正整數，且

  C

  0

  x

  =1．這是組合數

  C

  m

  n

  （n,m是正整數，且m≤n）的一種推廣．
  （1）計算：

  C

  3

  -

  7

  與

  C

  3

  -

  8

  +

  C

  2

  -

  8

  ；
  （2）猜想并證明：

  C

  m

  x

  +

  C

  m

  -

  1

  x

  =_____（用

  C

  m

  x

  的形式表示，其中x∈R，m是正整數）．
  組卷：11引用：3難度：0.5

  解析

• 22．設函數f（x）=axlnx,其中a∈R，曲線y=f（x）在點（1，f（1））處的切線經過點（3，2）．
  （Ⅰ）求a的值；
  （Ⅱ）求函數f（x）的極值；
  （Ⅲ）證明：f（x）＞

  x

  e

  x

  -

  2

  e

  ．
  組卷：815引用：5難度：0.5

  解析