2020-2021學年江蘇省泰州中學高一（下）第一次月考檢測數(shù)學試卷

一、單項選擇題（本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．若向量

  BA

  =（2，3），

  AC

  =（-4，-7），則

  BC

  =（　　）

  A．（-2，-4）

  B．（2，4）

  C．（6，10）

  D．（-6，-10）
  組卷：244引用：4難度：0.9

  解析

• 2．已知角α的終邊經(jīng)過點P（-3，4），則tan2α=（　　）

  A． 24 7

  B． 8 3

  C．- 8 3

  D．- 24 7
  組卷：432引用：6難度：0.9

  解析

• 3．在△ABC中，AD為BC邊上的中線，E為AD的中點，則

  EB

  =（　　）

  A． 3 4 AB - 1 4 AC

  B． 1 4 AB - 3 4 AC

  C． 3 4 AB + 1 4 AC

  D． 1 4 AB + 3 4 AC
  組卷：17627引用：170難度：0.9

  解析

• 4．α為第三象限的角，則

  1

  +

  cos

  2

  α

  cosα

  -

  1

  -

  cos

  2

  α

  sinα

  =（　　）

  A．0

  B．1

  C．-1

  D．2
  組卷：67引用：4難度：0.9

  解析

• 5．在△ABC中，

  A

  =

  π

  4

  ，

  B

  =

  π

  3

  ，BC=2，AC的垂直平分線交AB點D，則

  AC

  ?

  CD

  =（　　）

  A．-1

  B．-2

  C．3

  D．-3
  組卷：95引用：2難度：0.6

  解析

• 6．已知在△ABC中，

  cos

  （

  A

  -

  π

  6

  ）

  =

  -

  1

  3

  ，那么

  sin

  （

  A

  +

  π

  6

  ）

  +

  cos

  A

  等于（　　）

  A． - 3 3

  B． 3 3

  C． - 2 3 3

  D． 2 3 3
  組卷：269引用：4難度：0.7

  解析

• 7．若O是△ABC所在平面內(nèi)的一點，且滿足|

  OB

  -

  OC

  |=|

  OB

  +

  OC

  -2

  OA

  |，則△ABC的形狀是（　　）

  A．等邊三角形	B．等腰三角形
  C．等腰直角三角形	D．直角三角形
  組卷：443引用：31難度：0.7

  解析

四、解答題（本大題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知函數(shù)

  f

  （

  x

  ）

  =

  （

  3

  2

  a

  +

  b

  ）

  sinx

  +

  （

  1

  2

  a

  -

  3

  b

  ）

  cosx

  ，且f（0）=-1，

  f

  （

  π

  3

  ）

  =

  1

  ．
  （1）求f（x）的解析式；
  （2）已知g（x）=x²-2x+m-3，若對任意的x₁∈[0，π]，總存在x₂∈[-2，m]，使得f（x₁）=g（x₂）成立，求m的取值范圍．
  組卷：237引用：2難度：0.5

  解析

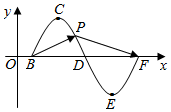• 22．已知函數(shù)f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的圖象如圖所示，點B，D，F(xiàn)為f（x）與x軸的交點，點C，E分別為f（x）的最高點和最低點，若將其圖象向右平移

  1

  2

  個單位后得到函數(shù)g（x）的圖象，而函數(shù)g（x）的最小正周期為4，且在x=0處取得最小值．
  （1）求參數(shù)ω和φ的值；
  （2）若A=1，求向量2

  BC

  -

  CD

  與向量

  BC

  +3

  CD

  之間夾角的余弦值；
  （3）若點P為f（x）函數(shù)圖象上的動點，當點P在C，E之間運動時，

  BP

  ?

  PF

  ≥1恒成立，求A的取值范圍．
  組卷：243引用：7難度：0.5

  解析