2022-2023學年廣東省惠州市惠陽區良井中學七年級（上）月考數學試卷（10月份）

一、選擇題（共10題，共30分）

• 1．已知a＞b,a＞c,若M=a²-ac,N=ab-bc,則M與N的大小關系是（　　）

  A．M＜N

  B．M=N

  C．M＞N

  D．不能確定
  組卷：1056引用：6難度：0.8

  解析

• 2．下列判斷正確的是（　　）

  A．3a2b與ba2不是同類項

  B．單項式-x3y2的系數是-1

  C． m 2 n 5 不是整式

  D．3x2-y+5xy2是二次三項式
  組卷：247引用：9難度：0.9

  解析

• 3．如圖是一組有規律的圖案，第1個圖案由5個基礎圖形組成，第2個圖案由8個基礎圖形組成，……，如果按照以下規律繼續下去，那么通過觀察，可以發現：第20個圖案需要（　　）個基本圖形．
  

  A．402

  B．404

  C．406

  D．408
  組卷：468引用：9難度：0.8

  解析

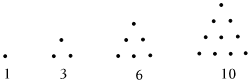• 4．古希臘的畢達哥拉斯學派認為：1，3，6，10，15，21，?這些數量的（石子），都可以排成三角形，像這樣的數稱為三角形，其中，1稱為第一個三角形數，3稱為第二個三角形數，以此類推，那么，第23個三角形數與第21個三角形數的差為（　　）

  A．23

  B．24

  C．45

  D．47
  組卷：10引用：2難度：0.5

  解析

• 5．按一定規律排列的單項式：a,-a²，a³，-a⁴，a⁵，-a⁶，…，第n個單項式是（　　）

  A．an

  B．-an

  C．（-1）n+1an

  D．（-1）nan
  組卷：2112引用：25難度：0.9

  解析

• 6．如圖，下面是按照一定規律畫出的“數形圖”，經觀察可以發現：圖A₂比圖A₁多出2個“樹枝”，圖A₃比圖A₂多出4個“樹枝”，圖A₄比圖A₃多出8個“樹枝”，……，照此規律，圖A₆比圖A₂多出的“樹枝”的個數是（　　）
  

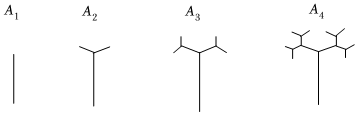
  A．28個

  B．56個

  C．60個

  D．124個
  組卷：41引用：4難度：0.7

  解析

• 7．為了求1+2+2²+2³+…+2²⁰¹¹+2²⁰¹²的值，可令S=1+2+2²+2³+…+2²⁰¹¹+2²⁰¹²，則2S=2+2²+2³+2⁴+…+2²⁰¹²+2²⁰¹³，因此2S-S=2²⁰¹³-1，所以1+2²+2³+…+2²⁰¹²=2²⁰¹³-1．仿照以上方法計算1+5+5²+5³+…+5²⁰¹²的值是（　　）

  A．52013-1

  B．52013+1

  C． 5 2013 - 4 4

  D． 5 2013 - 1 4
  組卷：14569引用：19難度：0.1

  解析

• 8．當x=1時，多項式ax⁵+bx³+cx-1的值是5，則當x=-1時，它的值是（　　）

  A．-7

  B．-3

  C．-5

  D．7
  組卷：507引用：6難度：0.6

  解析

三、解答題（共8題，共62分）

• 24．閱讀下列材料并解決問題：
  若一個正整數滿足：個位數字不為0，將原數各個數位上的數字從個位到高位依序重排得到一個新數，將新數與原數相加，所得的和能被15整除，則稱這個數為“優數”．
  例如：327是“優數”，因為327+723=1050，且1050÷15=70；35不是“優數”，因為35+53=88，而88不能被15整除．
  （1）判斷87、139是否為“優數”，并說明理由；
  （2）若一個三位正整數M是“優數”，且滿足個位數字大于百位數字，則稱M為“最優數”．請求出“最優數”的個數．
  組卷：1037引用：3難度：0.3

  解析

• 25．已知：△ABC中，BC=a,AC=b,AB=c,a是最小的合數，b、c滿足等式：|b-5|+（c-6）²=0，點P是△ABC的邊上一動點，點P從點B開始沿著△ABC的邊按BA→AC→CB順序順時針移動一周，回到點B后停止，移動的路徑為S，移動的速度為每秒3個單位．如圖1所示．
  （1）試求出△ABC的周長；
  （2）當點P移動到AC邊上時，化簡：|S-4|+|3S-6|+|4S-45|；
  （3）如圖2所示，若點Q是△ABC的邊上一動點，P、Q兩點分別從B、C同時出發，即當點P開始移動的時候，點Q從點C開始沿著△ABC的邊順時針移動，移動的速度為每秒5個單位，試問：當t為何值時，P、Q兩點的路徑（在三角形的邊上的距離）相差為3？此時點P在△ABC的哪條邊上？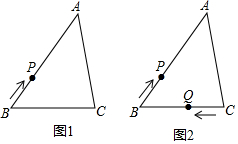
  
  組卷：274引用：3難度：0.5

  解析