2022-2023學年江蘇省宿遷市沭陽縣九年級（下）第五次調研數學試卷

一、選擇題：（本大題共8小題，每小題3分，共24分．在每小題所給出的四個選項中，恰有一項是符合題目要求的，請將正確選項前的字母代號填涂在答題卡相應位置上．）

• 1．方程x（x-1）=0的根是（　　）

  A．x=0

  B．x=1

  C．x1=0，x2=1

  D．x1=1，x2=-1
  組卷：419引用：13難度：0.7

  解析

• 2．已知⊙O的半徑為4cm.若點P到圓心O的距離為3cm,則點P（　　）

  A．在⊙O內

  B．在⊙O上

  C．在⊙O外

  D．無法確定
  組卷：514引用：4難度：0.8

  解析

• 3．某班有6個學習小組，每組的人數分別為3，4，5，6，6，7，這組數據的中位數是（　　）

  A．4

  B．5

  C．5.5

  D．6
  組卷：77引用：2難度：0.8

  解析

• 4．如圖，在△ABC中，點D，E分別為AB，AC的中點，若DE=2，則BC的長度為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：522引用：9難度：0.6

  解析

• 5．二次函數y=x²-2x圖象的頂點坐標是（　　）

  A．（1，1）

  B．（-1，1）

  C．（1，-1）

  D．（-1，-1）
  組卷：338引用：6難度：0.7

  解析

• 6．如圖，已知⊙O的內接四邊形ABCD，若∠ABC=125°，則∠AOC等于（　　）

  A．55°

  B．105°

  C．110°

  D．125°
  組卷：144引用：3難度：0.6

  解析

• 7．若關于x的一元二次方程x²+2x-（k-1）=0有實數根，則k的取值范圍是（　　）

  A．k＞0

  B．k≥0

  C．k＜0

  D．k≤0
  組卷：85引用：3難度：0.7

  解析

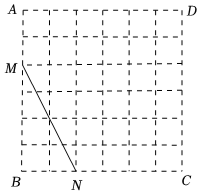• 8．如圖，在6×6的正方形網格圖形ABCD中，M，N分別是AB，BC上的格點，BM=4，BN=2．若點P是這個網格圖形中的格點，連接PM，PN，則所有滿足∠MPN=45°的△PMN中，DP的最小值是（　　）

  A． 3 2 - 10

  B．1

  C． 2

  D．2
  組卷：201引用：3難度：0.5

  解析

二、填空題：（本大題共10小題，每小題3分，共30分．不需寫出解答過程，請把答案直接填寫在答題卡相應位置上．）

• 9．若

  a

  4

  =

  b

  3

  ，則

  b

  a

  -

  b

  =

  ．
  組卷：91引用：3難度：0.9

  解析

三、解答題：（本大題共10小題，共76分．請在答題卡指定區域內作答，解答時應寫出文字說明、證明過程或演算步驟．）

• 27．如圖①，已知矩形ABCD，AB=6，AD=8．點E從點B出發，沿邊BC運動至點C停止．以DE為直徑作⊙O，⊙O與對角線AC交于點F，連接FD，FE．
  
  （1）如圖②，當E運動至終點C時，求

  FD

  FE

  的值；
  （2）試探究：在點E運動的過程中，

  FD

  FE

  的值是否為定值？若是，請求出這個值；若不是，請說明理由；
  （3）如圖③，以FD，FE為邊構造矩形DFEG，連接CG，求證：△ADF∽△CDG，并直接寫出在這一運動過程中，點G所經過的路徑長．
  組卷：133引用：3難度：0.1

  解析

• 28．定義：函數圖象上到兩坐標軸的距離都不大于n（n≥0）的點叫做這個函數圖象的“n階方點”．例如，點（1，1）是一次函數y=x圖象的“1階方點”．
  
  （1）在①（1，1），②

  （

  -

  2

  ，-

  1

  2

  ）

  ，③

  （

  -

  5

  2

  ，-

  2

  5

  ）

  三點中，是反比例函數

  y

  =

  1

  x

  圖象的“2階方點”的有

  （填序號）；
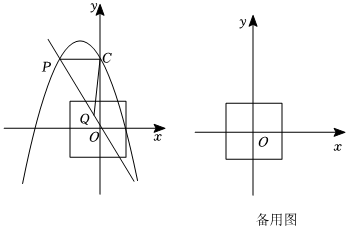
  （2）如圖，已知拋物線y=-（x+1）²+4交y軸于點C，一次函數y=ax+2a+3的圖象交拋物線第二象限于點P，點Q為該一次函數圖象的“1階方點”；
  ①求△PCQ的面積的最大值；
  ②若一次函數y=ax+2a+3圖象的“1階方點”有且只有一個，求a的值；
  （3）若拋物線y=-（x-m）²-2m+2的“m階方點”一定存在，求m的取值范圍．
  組卷：309引用：3難度：0.3

  解析