當前位置：試卷中心 > 試卷詳情

2023-2024學年北京市海淀區中關村中學高二（上）期中數學試卷

發布：2024/10/6 12:0:1

一、選擇題：本大題共10小題，每小題4分，共40分.在每小題列出的四個選項中，選出符合題目要求的一項.

1．已知
a
=（x,1，3），
b
=（1，3，9），如果
a
與
b
為共線向量，則x=（　　）
A．1 B．
1
2
C．
1
3
D．
1
6
組卷：119引用：3難度：0.8
解析
2．已知集合A={y|y=e^x}，集合B={x|y=ln（x-1）}，則A∪B=（　　）
A．R B．[1，+∞） C．（0，+∞） D．（1，+∞）
組卷：154引用：2難度：0.8
解析
3．已知直線m和平面α，β，則下列四個命題中正確的是（　　）
A．若α⊥β，m?β，則m⊥α B．若m∥α，m∥β，則α∥β
C．若α∥β，m∥α，則m∥β D．若α∥β，m⊥α，則m⊥β
組卷：152引用：10難度：0.7
解析
4．某校組織全體學生參加了主題為“建黨百年，薪火相傳”的知識競賽，隨機抽取了200名學生進行成績統計、發現抽取的學生的成績都在50分至100分之間，進行適當分組后（每組為左閉右開的區間），畫出頻率分布直方圖如圖所示，在被抽取的學生中，成績在區間[80，90）的學生數是（　　）
A．30 B．45 C．60 D．100
組卷：113引用：1難度：0.7
解析
5．已知兩條異面直線的方向向量分別是
u
=
（
3
，-
1
，
2
）
，
v
=
（
-
1
，
3
，
2
）
，則這兩條直線所成的角θ滿足（　　）
A．
sinθ
=
1
7
B．
cosθ
=
1
7
C．
sinθ
=
-
1
7
D．
cosθ
=
-
1
7
組卷：45引用：2難度：0.7
解析
6．已知平面
α
=
{
P
|
n
?
P
0
P
=
0
}
，其中P₀（1，1，1），法向量
n
=
（
-
1
，
1
，
2
）
，則下列各點中不在平面α內的是（　　）
A．（2，0，1） B．（2，0，2） C．（-1，1，0） D．（0，2，0）
組卷：178引用：4難度：0.8
解析
7．在棱長為1的正方體ABCD-A₁B₁C₁D₁中，M是線段B₁D₁上一點，則點M到平面A₁BD的距離是（　　）
A．
3
6
B．
3
3
C．
3
4
D．
6
3
組卷：50引用：2難度：0.5
解析
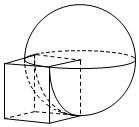8．如圖，將半徑為1的球與棱長為1的正方體組合在一起，使正方體的一個頂點正好是球的球心，則這個組合體的體積為（　　）
A．
7
6
π
+
1
B．
7
6
π
+
5
6
C．
7
8
π
+
1
D．π+1
組卷：479引用：7難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

五、解答題：本大題共2小題，共25分.

23．在△ABC中，
bsin
2
A
=
3
asin
B
．
（Ⅰ）求∠A；
（Ⅱ）若△ABC的面積為
3
3
，再從條件①、條件②、條件③這三個條件中選擇一個作為已知，使△ABC存在且唯一確定，求a的值．
條件①：
sin
C
=
2
7
7
；條件②：
b
c
=
3
3
4
；條件③：
cos
C
=
21
7

注：如果選擇的條件不符合要求，第（II）問得0分；如果選擇多個符合要求的條件分別解答，按第一個解答計分．
組卷：1156引用：12難度：0.6
解析
24．給定正整數n≥2，設集合M={α|α=（t₁，t₂，…，t_n），t_k∈{0，1}，k=1，2，…，n}．對于集合M中的任意元素β=（x₁，x₂，…，x_n）和γ=（y₁，y₂，…，y_n），記β?γ=x₁y₁+x₂y₂+…+x_ny_n．
設A?M，且集合A={α_i|α_i=（t_i1，t_i2，…，t_in），i=1，2，…，n}，對于A中任意元素α_i，α_j，若
α
i
?
α
j
=
p
,

i
=
j
,
1
，

i
≠
j
,
則稱A具有性質T（n,p）．
（Ⅰ）判斷集合A={（1，1，0），（1，0，1），（0，1，1）}是否具有性質T（3，2）？說明理由；
（Ⅱ）判斷是否存在具有性質T（4，p）的集合A，并加以證明；
（Ⅲ）若集合A具有性質T（n,p），證明：t_1j+t_2j+…+t_nj=p（j=1，2，…，n）．
組卷：467引用：6難度：0.1
解析