當前位置：試卷中心 > 試卷詳情

2022-2023學年北京師大附中高二（上）期末數學試卷

發布：2024/4/20 14:35:0

一、選擇題（每小題4分，共40分，每題均只有一個正確答案）

1．已知向量
a
=（-1，2，1），
b
=（3，x,y），且
a
∥
b
，那么xy=（　　）
A．-18 B．9 C．-9 D．18
組卷：306引用：3難度：0.9
解析
2．已知O為原點，點A（2，-2），以OA為直徑的圓的方程為（　　）
A．（x-1）²+（y+1）²=2 B．（x-1）²+（y+1）²=8
C．（x+1）²+（y-1）²=2 D．（x+1）²+（y-1）²=8
組卷：701引用：10難度：0.8
解析
3．已知雙曲線
x
2
m
-
y
2
=
1
的漸近線方程為
y
=±
1
2
x
，則實數m的值為（　　）
A．
1
4
B．4 C．-4 D．
-
1
4
組卷：169引用：1難度：0.7
解析
4．為拋物線y²=2px（p＞0）的焦點與橢圓
x
2
9
+
y
2
5
=
1
的一個焦點重合，則該拋物線的準線方程為（　　）
A．x=-1 B．x=1 C．x=2 D．x=-2
組卷：681引用：7難度：0.7
解析
5．已知直線l過點A（-3，1），且與直線x-2y+3=0垂直，則直線l的一般式方程為（　　）
A．2x+y+3=0 B．2x+y+5=0 C．2x+y-1=0 D．2x+y-2=0
組卷：292引用：5難度：0.8
解析
6．布達佩斯的伊帕姆維澤蒂博物館收藏的達?芬奇方磚，在正六邊形上畫了具有視覺效果的正方體圖案（如圖1），把三片這樣的達?芬奇方磚形成圖2的組合，這個組合表達了圖3所示的幾何體．如圖3中每個正方體的棱長為1，則點A到平面QGC的距離是（　　）
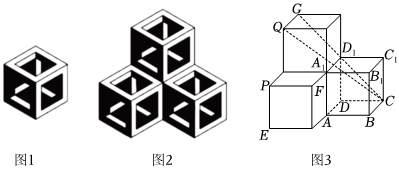
A．
1
4
B．
1
2
C．
2
2
D．
3
2
組卷：185引用：10難度：0.5
解析
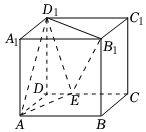7．如圖，在正方體ABCD-A₁B₁C₁D₁中，E是棱CD上的動點．則下列結論不正確的是（　　）
A．D₁E∥平面A₁B₁BA
B．EB₁⊥AD₁
C．直線AE與B₁D₁所成角的范圍為
（
π
4
，
π
2
）
D．二面角E-A₁B₁-A的大小為
π
4
組卷：628引用：8難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（共6小題，共85分．解答時寫出文字說明，演算步驟或證明過程）

20．已知拋物線E：x²=2py（p＞0）的焦點為F，A（2，y₀）是E上一點，且|AF|=2．
（1）求E的方程；
（2）設點B是E上異于點A的一點，直線AB與直線y=x-3交于點P，過點P作x軸的垂線交E于點M，證明：直線BM過定點．
組卷：637引用：8難度：0.6
解析
21．已知有限數列A：a₁，a₂，?，a_m為單調遞增數列．若存在等差數列B：b₁，b₂，?，b_m+1，對于A中任意一項a_i，都有b_i≤a_i＜b_i+1，則稱數列A是長為m的Ω數列．
（Ⅰ）判斷下列數列是否為Ω數列（直接寫出結果）：
①數列1，4，5，8；
②數列2，4，8，16．
（Ⅱ）若a＜b＜c（a,b,c∈R），證明：數列a,b,c為Ω數列；
（Ⅲ）設M是集合{x∈N|0≤x≤63}的子集，且至少有28個元素，證明：M中的元素可以構成一個長為4的Ω數列．
組卷：166引用：3難度：0.5
解析