2022-2023學年山西省太原五中八年級（下）月考數學試卷（3月份）

一、選擇題（共10小題，每題3分，共30分）

• 1．不等式x+2≥3的解集在數軸上表示正確的是（　　）

  A．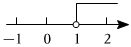

  B．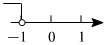

  C．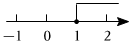

  D．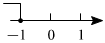
  組卷：427引用：3難度：0.6

  解析

• 2．已知點P（m-3，2）在第二象限，則m的取值范圍是（　　）

  A．m＞-3

  B．m＜-3

  C．m＞3

  D．m＜3
  組卷：274引用：5難度：0.7

  解析

• 3．已知△ABC的三條邊分別為a,b,c,下列條件不能判斷△ABC是直角三角形的是（　　）

  A．a2=b2-c2	B．a=6，b=8，c=10
  C．∠A=∠B+∠C	D．∠A：∠B：∠C=5：12：13
  組卷：1136引用：13難度：0.7

  解析

• 4．如圖，AC=CD=DA=BC=DE．則∠BAE是∠BAC的（　　）

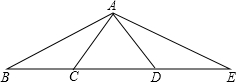
  A．4倍

  B．3倍

  C．2倍

  D．1倍
  組卷：426引用：4難度：0.9

  解析

• 5．2月份的研學活動，對于初二的全體同學是難得且有意義的，我校租用55座和53座兩種型號的客車接送同學們，若租用55座客車x輛，租用53座客車y輛，則不等式“55x+53y≥990”表示的實際意義是（　　）

  A．兩種客車總的載客量不少于990人

  B．兩種客車總的載客量不超過990人

  C．兩種客車總的載客量不足990人

  D．兩種客車總的載客量恰好等于990人
  組卷：500引用：3難度：0.9

  解析

• 6．下列命題中，逆命題是真命題的有（　　）
  （1）兩直線平行，同旁內角互補；（2）在同一平面內，垂直于同一直線的兩直線平行；（3）相等的角是內錯角；（4）有一個角是60°的等腰三角形是等邊三角形．

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：156引用：2難度：0.6

  解析

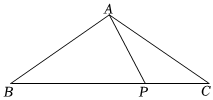• 7．如圖，在△ABC中，∠A=120°，AB=AC=2

  3

  cm,點P從點B開始以1cm/s的速度向點C移動，當△ABP為直角三角形時，則運動的時間為（　　）

  A．3s

  B．3s或4s

  C．1s或4s

  D．2s或3s
  組卷：1675引用：7難度：0.5

  解析

三、解答題（本大題共8個小題，共55分）

• 22．（1）閱讀理解“|a|”的幾何意義是：數a在數軸上對應的點到原點的距離，所以“|a|≥2”可理解為：數a在數軸上對應的點到原點的距離不小于2，則：
  ①“|a|＜2”可理解為

  ；
  ②請列舉兩個符號不同的整數，使不等式“|a|＞2”成立，列舉的a的值為

  ．
  我們定義：形如“|x|≤m,|x|≥m,|x|＜m,|x|＞m”（m為非負數）的不等式叫做絕對值不等式，能使一個絕對值不等式成立的所有未知數的值稱為絕對值不等式的解集．
  （2）理解應用：根據絕對值的幾何意義可以解一些絕對值不等式．
  
  由圖可以得出：絕對值不等式|x|＞1的解集是x＜-1或x＞1，絕對值不等式|x|≤3的解集是-3≤x≤3．則：
  ①不等式|x|≥4的解集是

  ．
  ②不等式

  |

  1

  2

  x

  |

  ＜

  2

  的解集是

  ．
  組卷：583引用：2難度：0.7

  解析

• 23．如圖1，AB=AC，∠BAC=90°，直線AE是經過點A的直線，BD⊥AE于D，CE⊥AE于E，則△ADB≌△CEA．
  （1）[線形訓練]如圖2，Rt△ABC中，AB=AC，∠BAC=90°，直線AE是經過點A的任一直線，BD⊥AE于D，CE⊥AE于E，證明：BD=DE+CE．
  （2）[問題創設]如圖3，在△ABC中，AB=AC，若頂點A在直線m上，點D，E也在直線m上，如果∠BAC=∠ADB=∠AEC=100°，那么（1）中結論還成立嗎？如果不成立，BD，DE，CE三條線段之間有怎樣的數量關系？直接寫出結論．
  （3）[發散探究]如圖4，把等腰直角三角板放在黑板上畫好了的平面直角坐標系內，已知直角頂點H在y軸正半軸上，頂點G在第一象限且使其橫、縱坐標始終相等，若另一頂點K（a,-2a+6）落在第四象限，求a的值．
  
  組卷：239引用：4難度：0.3

  解析