2021-2022學年寧夏銀川市唐徠回民中學高一（下）期末數學試卷

一、選擇題：本題共12小題，每小題5分，共計60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．若集合M={x|log₂（x-1）≤1}，則下列結論正確的是（　　）

  A．M=（-∞，3]

  B． 3 ? M

  C． { 3 } ∈ M

  D． { 3 } ? M
  組卷：228引用：2難度：0.7

  解析

• 2．函數y=x²-x+1，x∈[-1，1]的最大值與最小值之和為（　　）

  A．1.75

  B．3.75

  C．4

  D．5
  組卷：367引用：3難度：0.8

  解析

• 3．如果一個正方體的棱長與一個球的半徑相等，那么它們的表面積之比是（　　）

  A． 3 2 π

  B． 4 π 3

  C． 3 4 π

  D． 3 π 2
  組卷：119引用：1難度：0.8

  解析

• 4．直線ax-y+2a=0與圓x²+y²=9的位置關系是（　　）

  A．相離

  B．相交

  C．相切

  D．不確定
  組卷：1050引用：34難度：0.9

  解析

• 5．已知

  a

  =（1，sin²x），

  b

  =（2，sin2x），其中x∈（0，π）．若|

  a

  ?

  b

  |=|

  a

  |?|

  b

  |，則tanx的值等于（　　）

  A．1

  B．-1

  C． 3

  D． 2 2
  組卷：103引用：8難度：0.9

  解析

• 6．把函數y=sinx的圖象上所有點的橫坐標都縮小到原來的一半，縱坐標保持不變，再把圖象向左平移

  π

  4

  個單位，這時對應于這個圖象的解析式為（　　）

  A．y=cos2x	B．y=-sin2x
  C． y = sin （ 2 x - π 4 ）	D． y = sin （ 2 x + π 4 ）
  組卷：98引用：21難度：0.9

  解析

• 7．記S_n為等差數列{a_n}的前n項和．已知S₄=0，a₅=5，則（　　）

  A．an=2n-5

  B．an=3n-10

  C．Sn=2n2-8n

  D．Sn= 1 2 n2-2n
  組卷：12271引用：27難度：0.9

  解析

三、解答題（本題包括六道小題共計70分）

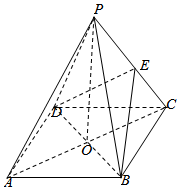• 21．如圖所示，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，底面邊長為a,E是PC的中點．
  （Ⅰ）求證：PA∥平面BDE；
  （Ⅱ）平面PAC⊥平面BDE；
  （Ⅲ）若二面角E-BD-C為30°，求四棱錐P-ABCD的體積．
  組卷：384引用：6難度：0.6

  解析

• 22．已知函數f（x）=sinx+cosx.
  （1）若f（x）=2f（-x），求

  co

  s

  2

  x

  -

  sinxcosx

  1

  +

  si

  n

  2

  x

  的值；
  （2）求函數F（x）=f（x）?f（-x）+f²（x）的最大值和單調遞增區間．
  組卷：229引用：3難度：0.3

  解析