2023-2024學年江蘇省蘇州市姑蘇區振華中學九年級（上）月考數學試卷（10月份）
發布：2024/9/12 10:0:8
一、選擇題（共8小題，每題3分，共24分）
-
1．下列各式中，y是x的二次函數是（ ）
組卷：423引用：4難度：0.8 -
2．拋物線y=-2（x-2）2+3的頂點坐標是（ ）
組卷：250引用：6難度：0.6 -
3．若關于x的一元二次方程x2-2x-k=0沒有實數根，則k的取值范圍是（ ）
組卷：1276引用：49難度：0.9 -
4．在二次函數y=-（x+1）2+2的圖象中，若y隨x的增大而增大，則x的取值范圍是（ ）
組卷：1048引用：4難度：0.6 -
5．在“新冠”初期，有1人感染了“新冠”，經過兩輪傳染后共有324人感染了“新冠”（這兩輪感染均未被發現未被隔離），則每輪傳染中平均一個人傳染了幾個人？設每輪傳染中平均一個人傳染了x人，則根據題意可列方程（ ）
組卷：174引用：1難度：0.5 -
6．拋物線y=-x2+bx+3的對稱軸為直線x=-1，若關于x的一元二次方程-x2+bx+3-t=0（t為實數）在-2＜x＜3的范圍內有實數根，則t的取值范圍是（ ）
組卷：5162引用：24難度：0.3 -
7．拋物線y=（m+1）x2+2mx+3上有兩點A（-3，y1）、B（5，y2）、C點（x0，y0）為此拋物線頂點且y1＞y2≥y0，則m的取值范圍為（ ）
組卷：588引用：3難度：0.5 -
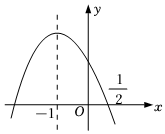8．如圖，拋物線y=ax2+bx+c的對稱軸為直線x=-1，且過點（，0），有下列結論：①abc＞0；②a-2b+4c＞0；③25a-10b+4c=0；④3b+2c＞0；其中正確的結論有（ ）12組卷：423引用：3難度：0.5
二、填空題（共8小題，每題3分，共24分）
-
9．關于x的方程x2=x的解是 ．
組卷：49引用：3難度：0.7
三、解答題（共11小題，共82分）
-
26．定義：如果二次函數y=a1x2+b1x+c1（a1≠0，a1，b1，c1是常數）與y=a2x2+b2x+c2（a2≠0，a2，b2，c2是常數）滿足a1+a2=0，b1=b2，c1+c2=0，則這兩個函數互為“N”函數．
（1）寫出y=-x2+x-1的“N”函數的表達式；
（2）若題（1）中的兩個“N”函數與正比例函數y=kx（k≠0）的圖象只有兩個交點，求k的值；
（3）如圖，二次函數y1與y2互為“N”函數，A、B分別是“N”函數y1與y2圖象的頂點，C是“N”函數y2與y軸正半軸的交點，連接AB、AC、BC，若點A（-2，1）且△ABC為直角三角形，求點C的坐標．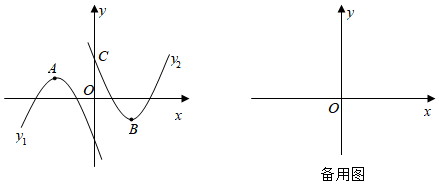
組卷：971引用：5難度：0.1 -
27．綜合與實踐
問題提出
某興趣小組開展綜合實踐活動：在Rt△ABC中，∠C=90°，D為AC上一點，CD=，動點P以每秒1個單位的速度從C點出發，在三角形邊上沿C→B→A勻速運動，到達點A時停止，以DP為邊作正方形DPEF．設點P的運動時間為t s,正方形DPEF的面積為S，探究S與t的關系．2
初步感知
（1）如圖1，當點P由點C運動到點B時，
①當t=1時，S=；
②S關于t的函數解析式為 ．
（2）當點P由點B運動到點A時，經探究發現S是關于t的二次函數，并繪制成如圖2所示的圖象．請根據圖象信息，求S關于t的函數解析式及線段AB的長．
延伸探究
（3）若存在3個時刻t1，t2，t3（t1＜t2＜t3）對應的正方形DPEF的面積均相等．
①t1+t2=；
②當t3=4t1時，求正方形DPEF的面積．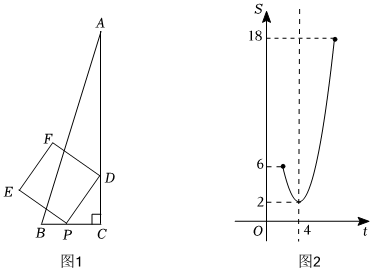
組卷：3482引用：27難度：0.3