2023-2024學年湖北省武漢市漢陽區八年級(上)期中數學試卷
發布:2024/10/10 4:0:1
一、選擇題(每小題3分,共30分)
-
1.下列四個交通標識圖案中,是軸對稱圖案的是( )
A. 
B. 
C. 
D.  組卷:9引用:1難度:0.8
組卷:9引用:1難度:0.8 -
2.作三角形ABC的一條高,其中正確的是?( )
A. 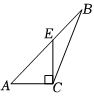
B. 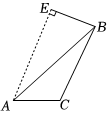
C. 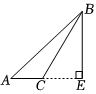
D. 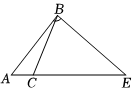 組卷:48引用:4難度:0.8
組卷:48引用:4難度:0.8 -
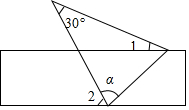 3.如圖,將一張含有30°角的三角形紙片的兩個頂點疊放在矩形的兩條對邊上,若∠2=44°,則∠1的大小為( )
3.如圖,將一張含有30°角的三角形紙片的兩個頂點疊放在矩形的兩條對邊上,若∠2=44°,則∠1的大小為( )A.14° B.16° C.90°-α D.α-44° 組卷:2927引用:34難度:0.9 -
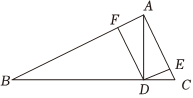 4.在ABC中,∠BAC=90°,AC≠AB,AD是斜邊BC上的高,DE⊥AC于E,DF⊥AB于F,如圖,則圖中與∠B(∠B除外)相等的角的個數是( )
4.在ABC中,∠BAC=90°,AC≠AB,AD是斜邊BC上的高,DE⊥AC于E,DF⊥AB于F,如圖,則圖中與∠B(∠B除外)相等的角的個數是( )A.3 B.4 C.5 D.6 組卷:75引用:1難度:0.7 -
5.一張正方形紙片經過兩次對折,并在如圖位置上剪去一個小正方形,打開后是( )
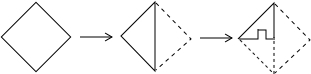
A. 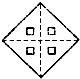
B. 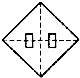
C. 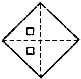
D. 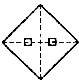 組卷:148引用:20難度:0.9
組卷:148引用:20難度:0.9 -
6.如果一個多邊形的內角和是外角和的3倍,則這個多邊形的邊數是( )
A.8 B.9 C.10 D.11 組卷:3122引用:26難度:0.7 -
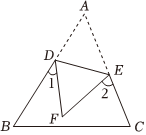 7.如圖,將三角形紙片ABC沿DE折疊,點A落在點F處,已知∠1+∠2=100°,則∠A的度數為( )
7.如圖,將三角形紙片ABC沿DE折疊,點A落在點F處,已知∠1+∠2=100°,則∠A的度數為( )A.80° B.100° C.50° D.以上都不對 組卷:309引用:6難度:0.7 -
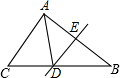 8.如圖:△ABC中,D為BC上一點,△ACD的周長為12cm,DE是線段AB的垂直平分線,AE=5cm,則△ABC的周長是( )
8.如圖:△ABC中,D為BC上一點,△ACD的周長為12cm,DE是線段AB的垂直平分線,AE=5cm,則△ABC的周長是( )A.17cm B.22cm C.29cm D.32cm 組卷:179引用:8難度:0.9
三、解答題(共8小題,共72分)
-
23.問題的提出:如圖1,△ABC中,AB=AC,求證:∠B=∠C.
知識的運用:如圖2,四邊形ABCD是正方形,AB=BC=CD=AD,∠ABC=∠BCD=∠ADC=90°,點E是邊BC上一點,∠AEF=90°,且EF=AE,連CF.求∠ECF的度數.
拓展與延伸:如圖3,四邊形ABCD中,AB=BC=CD=AD,AD∥BC,AB∥CD,E為四邊形ABCD邊BC上一點,連AE,若AE=EF,且∠AEF=∠ABC=α(α≥90°),探究∠DCF與α的數量關系.直接寫出結果,不需說明理由.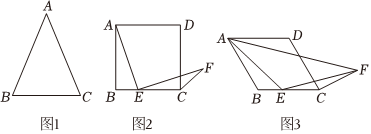 組卷:312引用:2難度:0.6
組卷:312引用:2難度:0.6 -
24.數學問題:如圖1,△ABC的中線AD、BE交于P點,試探究線段AP與PD間的數量關系,并說明理由,
數學思考:如圖2,△ABC的中線AD、BE交于P點,連DE,
(1)求證:.DE=12AB
(2)求證:∠ABC=∠EDC.
數學運用:
①如圖3,在四邊形ABCD中,AB∥CD,AB<CD,E、F分別是AD、BC邊的中點,直接寫出AB、CD與EF間的數量關系,不需要說明理由.
②如圖4,現有一塊四邊形紙片ABCD,AB∥CD,AD=CB,P、Q分別為AD、BC中點,EF∥MN∥AB,P、Q也同時是EM、FN的中點.現若有AB=m,CD=n,E或F點到MN的距離為h,請直接寫出四邊形EFNM的面積(用m、n、h表示). 組卷:118引用:1難度:0.5
組卷:118引用:1難度:0.5


