當(dāng)前位置：試卷中心 > 試卷詳情

2023-2024學(xué)年遼寧省沈陽(yáng)市小三校高三（上）聯(lián)考數(shù)學(xué)試卷（10月份）

發(fā)布：2024/9/26 10:0:2

一、選擇題。本題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

1．已知集合
A
=
{
x
|
5
-
x
x
≥
0
}
，集合B={x|y=lg（4-x）}，則A∪（?_RB）=（　　）
A．（0，4） B．[0，4） C．（0，+∞） D．[4，5]
組卷：158引用：3難度：0.8
解析
2．已知復(fù)數(shù)
z
=
1
-
i
2023
1
-
i
，則
z
-
z
=（　　）
A．-2i B．2i C．0 D．2
組卷：159引用：4難度：0.8
解析
3．已知命題p：?x∈R，mx²-2mx+1＜0是假命題，則實(shí)數(shù)m的取值范圍為（　　）
A．[0，1] B．（0，1]
C．（-∞，0）∪（1，+∞） D．（-∞，0]∪[1，+∞）
組卷：100引用：4難度：0.8
解析
4．已知函數(shù)
f
（
x
）
=
a
1
-
ax
（a＞0且a≠1）在區(qū)間[2，3]上單調(diào)遞增，則a的取值范圍為（　　）
A．
（
0
，
1
2
]
B．（1，+∞） C．
（
0
，
1
3
]
D．
[
1
3
，
1
2
]
組卷：125引用：8難度：0.8
解析
5．在△ABC中，D，E分別是邊BC和AC上的點(diǎn)，且
BD
=
2
DC
，
CE
=
2
EA
，BE與AD交于點(diǎn)F，記
CA
=
a
，
CB
=
b
，則
CF
=（　　）
A．
4
7
a
+
1
7
b
B．
1
7
a
+
4
7
b
C．
1
5
a
+
8
15
b
D．
8
15
a
+
1
5
b
組卷：64引用：1難度：0.7
解析
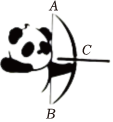6．2023年8月8日，第31屆世界大學(xué)生夏季運(yùn)動(dòng)會(huì)（成都世界大學(xué)生運(yùn)動(dòng)會(huì)）完美收官．在倒計(jì)時(shí)100天時(shí)，成都大運(yùn)會(huì)發(fā)布了官方體育圖標(biāo)——“十八墨寶”．這組“水墨熊貓”以大熊貓“奇一”為原型，將中國(guó)體育與中國(guó)書畫、中國(guó)國(guó)寶的融合做到了極致．“十八般武藝”造就“十八墨寶”，花式演繹十八項(xiàng)體育競(jìng)技，代表了體操、游泳、羽毛球等18個(gè)成都大運(yùn)會(huì)競(jìng)賽項(xiàng)目，深受廣大人民喜愛．其中，射箭的水墨熊貓以真實(shí)的射箭運(yùn)動(dòng)為原型，拉滿弓箭時(shí)，弓臂為圓弧形，弧中點(diǎn)到弦中點(diǎn)的距離為2cm,弦長(zhǎng)為8cm,則弓形的面積約為（參考數(shù)據(jù)：sin74°≈0.96，π≈3.14）（　　）
A．8.2cm² B．9.1cm² C．11.1cm² D．4.1cm²
組卷：78引用：5難度：0.7
解析

7．將4個(gè)編號(hào)為1，2，3，4的小球放入4個(gè)編號(hào)為1，2，3，4的盒子中，下列說(shuō)法正確的是（　　）

A．已知4號(hào)盒子為空盒子，其他盒子均有球，且每個(gè)小球的編號(hào)與盒子編號(hào)均不相同，則共有9種不同的放法

B．把4個(gè)不同的小球換為4個(gè)相同的小球，恰有1個(gè)空盒，有9種不同的放法

C．把4個(gè)不同的小球換為15個(gè)相同的小球，每個(gè)盒子的球數(shù)不少于其編號(hào)數(shù)，則共有52種不同的放法

D．每個(gè)盒內(nèi)至多放1個(gè)球，有24種不同的放法

組卷：29引用：1難度：0.7

解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部?jī)?nèi)容及下載

四、解答題。本題共6小題，共70分。解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟。

21．第33屆夏季奧林匹克運(yùn)動(dòng)會(huì)即將于2024年在巴黎舉辦，其中游泳比賽分為預(yù)賽、半決賽和決賽三個(gè)階段，只有預(yù)賽、半決賽都獲勝才有資格進(jìn)入決賽．已知甲在預(yù)賽和半決賽中獲勝的概率分別為
1
2
和
2
3
，乙在預(yù)賽和半決賽中獲勝的概率分別為
2
3
和
3
4
，丙在預(yù)賽和半決賽中獲勝的概率分別為p和
4
3
-
p
，其中
1
3
＜
p
＜
2
3
．
（1）甲、乙、丙三人中，哪個(gè)人進(jìn)入決賽的可能性更大？
（2）如果甲、乙、丙三人中恰有兩人進(jìn)入決賽的概率為
11
36
，求p的值；
（3）在（2）的條件下，設(shè)甲、乙、丙三人中進(jìn)入決賽的人數(shù)為ξ，求ξ的分布列．
組卷：226引用：1難度：0.5
解析
22．已知函數(shù)f（x）=sinx+x-2ln（x+1）．
（1）求證：當(dāng)
x
∈
（
0
，
π
2
）
時(shí)，f（x）＞0；
（2）求證：
1
2
ln
（
n
+
1
）
＜
sin
1
2
+
sin
1
4
+
?
+
sin
1
2
n
＜
1
2
×
（
1
+
1
2
+
1
3
+
?
+
1
n
）
（
n
∈
N
*
）
．
組卷：91引用：6難度：0.4
解析

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測(cè)評(píng) 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會(huì)員，資源免費(fèi)下載

A．[0，1]	B．（0，1]
C．（-∞，0）∪（1，+∞）	D．（-∞，0]∪[1，+∞）

2023-2024學(xué)年遼寧省沈陽(yáng)市小三校高三（上）聯(lián)考數(shù)學(xué)試卷（10月份）

一、選擇題。本題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

1．已知集合A={x|5-xx≥0}，集合B={x|y=lg（4-x）}，則A∪（?RB）=（ ）

2．已知復(fù)數(shù)z=1-i20231-i，則z-z=（ ）

3．已知命題p：?x∈R，mx2-2mx+1＜0是假命題，則實(shí)數(shù)m的取值范圍為（ ）

4．已知函數(shù)f（x）=a1-ax（a＞0且a≠1）在區(qū)間[2，3]上單調(diào)遞增，則a的取值范圍為（ ）

5．在△ABC中，D，E分別是邊BC和AC上的點(diǎn)，且BD=2DC，CE=2EA，BE與AD交于點(diǎn)F，記CA=a，CB=b，則CF=（ ）

7．將4個(gè)編號(hào)為1，2，3，4的小球放入4個(gè)編號(hào)為1，2，3，4的盒子中，下列說(shuō)法正確的是（ ）

四、解答題。本題共6小題，共70分。解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟。

22．已知函數(shù)f（x）=sinx+x-2ln（x+1）．（1）求證：當(dāng)x∈（0，π2）時(shí)，f（x）＞0；（2）求證：12ln（n+1）＜sin12+sin14+?+sin12n＜12×（1+12+13+?+1n）（n∈N*）．

1．已知集合
A
=
{
x
|
5
-
x
x
≥
0
}
，集合B={x|y=lg（4-x）}，則A∪（?_RB）=（　　）

2．已知復(fù)數(shù)
z
=
1
-
i
2023
1
-
i
，則
z
-
z
=（　　）

3．已知命題p：?x∈R，mx²-2mx+1＜0是假命題，則實(shí)數(shù)m的取值范圍為（　　）

4．已知函數(shù)
f
（
x
）
=
a
1
-
ax
（a＞0且a≠1）在區(qū)間[2，3]上單調(diào)遞增，則a的取值范圍為（　　）

5．在△ABC中，D，E分別是邊BC和AC上的點(diǎn)，且
BD
=
2
DC
，
CE
=
2
EA
，BE與AD交于點(diǎn)F，記
CA
=
a
，
CB
=
b
，則
CF
=（　　）

7．將4個(gè)編號(hào)為1，2，3，4的小球放入4個(gè)編號(hào)為1，2，3，4的盒子中，下列說(shuō)法正確的是（　　）

22．已知函數(shù)f（x）=sinx+x-2ln（x+1）．
（1）求證：當(dāng)
x
∈
（
0
，
π
2
）
時(shí)，f（x）＞0；
（2）求證：
1
2
ln
（
n
+
1
）
＜
sin
1
2
+
sin
1
4
+
?
+
sin
1
2
n
＜
1
2
×
（
1
+
1
2
+
1
3
+
?
+
1
n
）
（
n
∈
N
*
）
．