2023-2024學年浙江省金華市蘭溪市聚仁中學九年級（上）期中數學試卷

一、選擇題

• 1．已知3a=4b（ab≠0），則下列各式正確的是（　　）

  A． a b = 4 3

  B． a b = 3 4

  C． a 3 = b 4

  D． a 3 = 4 b
  組卷：418引用：14難度：0.8

  解析

• 2．下列成語所描述的事件中，是隨機事件的是（　　）

  A．水漲船高

  B．水中撈月

  C．一步登天

  D．一箭雙雕
  組卷：118引用：4難度：0.7

  解析

• 3．已知拋物線y=ax²-2ax+3（a＞0），A（-1，y₁），B（2，y₂），C（4，y₃）是拋物線上三點，則y₁，y₂，y₃由小到大的排列是（　　）

  A．y1＜y2＜y3

  B．y2＜y1＜y3

  C．y3＜y1＜y2

  D．y2＜y3＜y1
  組卷：2010引用：18難度：0.5

  解析

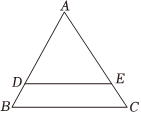• 4．如圖，在△ABC中，D是AB邊上一點，過點D作DE∥BC交AC于點E，若AD：DB=3：1，則S_△ADE：S_△ABC的值為（　　）

  A． 3 7

  B． 3 4

  C． 16 9

  D． 9 16
  組卷：458引用：4難度：0.5

  解析

• 5．如圖，AB是半圓O的直徑，∠BAC=28°，則∠D的度數是（　　）
  

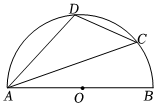
  A．62°

  B．118°

  C．152°

  D．138°
  組卷：315引用：3難度：0.5

  解析

• 6．如圖，在同一平面直角坐標系中，二次函數y=ax²+bx+c（a≠0）與一次函數y=acx+b的圖象可能是（　　）

  A．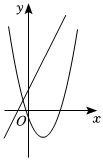

  B．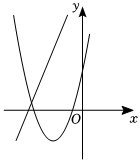

  C．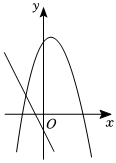

  D．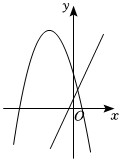
  組卷：1854引用：10難度：0.5

  解析

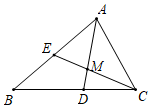• 7．如圖，在△ABC中，AD是∠BAC的平分線，CE與AD交于點M，∠ACE=∠B，下列結論中不正確的是（　　）

  A．△ACM∽△ABD

  B．△ACE∽△ABC

  C．△AEM∽△CDM

  D．△AEM∽△ACD
  組卷：569引用：6難度：0.6

  解析

• 8．在平面直角坐標系中，有兩條拋物線關于x軸對稱，且它們的頂點相距8個單位長度．若其中一條拋物線的函數表達式為y=x²-6x+m,則m的值是（　　）

  A．-5或-13

  B．-1或19

  C．5或13

  D．4或14
  組卷：97引用：2難度：0.6

  解析

三、解答題

• 23．定義：若一個四邊形能被其中的一條對角線分割成兩個相似三角形，則稱這個四邊形為“師梅四邊形”，這條對角線稱為“師梅線”．我們熟知的平行四邊形就是“師梅四邊形”．
  
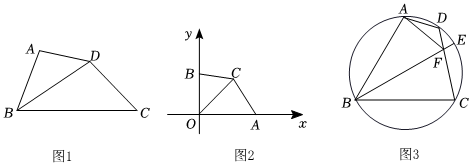
  （1）如圖1，BD平分∠ABC，

  BD

  =

  4

  2

  ，BC=10．四邊形ABCD是被BD分割成的“師梅四邊形”，求AB長；
  （2）如圖2，平面直角坐標系中，A、B分別是x軸和y軸上的點，且OA=3，OB=2，若點C是直線y=x在第一象限上的一點，且OC是四邊形OACB的“師梅線”，求四邊形OACB的面積；
  （3）如圖3，圓內接四邊形ABCD中，∠ABC=60°，點E是

  ?

  AC

  的中點，連接BE交CD于點F，連接AF，∠DAF=30°，
  ①求證：四邊形ABCF是“師梅四邊形”；
  ②若△ABC的面積為

  6

  3

  ，求線段BF的長．
  組卷：1175引用：9難度：0.1

  解析

• 24．已知拋物線y=x²+mx-2與x軸交于A、B兩點，與y軸交于點C，點A坐標為（-2，0）
  
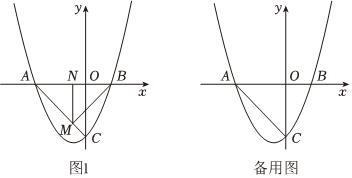
  （1）求拋物線的解析式及B、C兩點的坐標．
  （2）若點M是線段AC上一個動點（不與A、C重合），點N是線段AB上一個動點，設AN=t（t＞0）．
  ①如圖1，當點N運動到AB的中點時，作MN∥y軸交AC于點M．求證：∠BMN=∠BAC．
  ②當點N在運動過程中，在x軸上方的拋物線上是否存在點G，使得∠GNB=∠BAC且GN恰好平分∠AGB？若存在，求出此時點G的橫坐標和t的值；若不存在，請說明理由．
  組卷：165引用：1難度：0.3

  解析