當前位置：試卷中心 > 試卷詳情

2022-2023學年江蘇省鹽城市高三（上）段考數學試卷（11月份）

發布：2024/7/23 8:0:8

一、單項選擇題：共8題，每題5分，共40分.每題只有一個選項最符合題意.

1．命題“?x∈R，x²-x+1=0”的否定為（　　）
A．?x∈R，x²-x+1≠0 B．?x∈R，x²-x+1=0
C．?x∈R，x²-x+1≠0 D．?x?R，x²-x+1≠0
組卷：146引用：4難度：0.8
解析
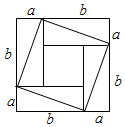2．無字證明是指禁用圖象而無需文字解釋就能不證自明的數學命題，由于其不證自明的特性，這種證明方式被認為比嚴格的數學證明更為優雅與條理，如圖，請寫出該圖驗證的不等式（　　）
A．a²+b²≥a+b B．4ab≥a²+b² C．
a
+
b
≥
2
ab
D．a²+b²≥2ab
組卷：159引用：5難度：0.5
解析
3．專家對某地區新冠肺炎爆發趨勢進行研究發現，從確診第一名患者開始累計時間t（單位：天）與病情爆發系數f（t）之間，滿足函數模型：f（t）=
1
1
+
e
-
0
.
22
（
t
-
50
）
，當f（t）=0.1時，標志著疫情將要大面積爆發，則此時t約為（　　）（參考數據：e^1.1≈3）
A．38 B．40 C．45 D．47
組卷：297引用：11難度：0.7
解析
4．衡量曲線彎曲程度的重要指標是曲率，曲線的曲率定義如下：若f'（x）是f（x）的導函數，f″（x）是f'（x）的導函數，則曲線y=f（x）在點（x,f（x））處的曲率
K
=
|
f
″
（
x
）
|
（
1
+
[
f
′
（
x
）
]
2
）
3
2
?
已知f（x）=lnx-cos（x-1），則曲線y=f（x）在點（1，f（1））處的曲率為（　　）
A．0 B．
2
4
C．
2
2
D．
2
組卷：104引用：4難度：0.8
解析
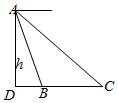5．如圖，從高為h的氣球（A）上測量待建規劃鐵橋（BC）的長，如果測得橋頭（B）的俯角是α，橋頭（C）的俯角是β，則橋BC的長為（　　）
A．
sin
（
α
-
β
）
sinαsinβ
h B．
cos
（
α
-
β
）
sinαsinβ
h
C．
sin
（
α
-
β
）
cosαcosβ
h D．
cos
（
α
-
β
）
cosαcosβ
h
組卷：64引用：8難度：0.7
解析
6．函數f（x）=cos（πx+φ）（0＜φ＜
π
2
）的部分圖象如圖所示，若方程f（x）=a在（0，x₀）上有兩個不同的實數解x₁，x₂，則x₁f（x₁）+x₂f（x₂）的取值范圍是（　　）
A．{0} B．（-1，
2
2
） C．（-
3
2
，
3
2
4
） D．（-
4
3
，
3
2
4
）
組卷：329引用：2難度：0.6
解析
7．已知數列{a_n}的通項公式是
a
n
=
n
2
sin
（
2
n
+
1
2
π
）
，則a₁+a₂+a₃+…+a₁₂=（　　）
A．0 B．55 C．66 D．78
組卷：134引用：2難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟

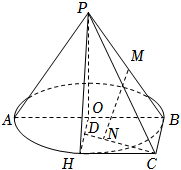21．如圖，P為圓錐的頂點，O為圓錐底面的圓心，圓錐的底面直徑AB=4，母線PH=2
2
，M是PB的中點，四邊形OBCH為正方形．
（1）設平面POH∩平面PBC=l；證明：l∥BC；
（2）設D為OH的中點，N是線段CD上的一個點，當MN與平面PAB所成角最大時，求MN的長．
組卷：304引用：9難度：0.5
解析
22．已知函數
f
（
x
）
=
x
-
1
x
-
alnx
（
a
∈
R
）
．
（1）若函數f（x）在（2，+∞）上單調遞增，求a的取值范圍；
（2）若函數f（x）有兩個不同的極值點x₁，x₂（x₁＞x₂），不等式f（x₁）＜mx₂恒成立，求實數m的取值范圍．
組卷：99引用：4難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．?x∈R，x²-x+1≠0	B．?x∈R，x²-x+1=0
C．?x∈R，x²-x+1≠0	D．?x?R，x²-x+1≠0

A． sin （ α - β ） sinαsinβ h	B． cos （ α - β ） sinαsinβ h
C． sin （ α - β ） cosαcosβ h	D． cos （ α - β ） cosαcosβ h

2022-2023學年江蘇省鹽城市高三（上）段考數學試卷（11月份）

一、單項選擇題：共8題，每題5分，共40分.每題只有一個選項最符合題意.

1．命題“?x∈R，x2-x+1=0”的否定為（ ）

2．無字證明是指禁用圖象而無需文字解釋就能不證自明的數學命題，由于其不證自明的特性，這種證明方式被認為比嚴格的數學證明更為優雅與條理，如圖，請寫出該圖驗證的不等式（ ）

5．如圖，從高為h的氣球（A）上測量待建規劃鐵橋（BC）的長，如果測得橋頭（B）的俯角是α，橋頭（C） 的俯角是β，則橋BC的長為（ ）

6．函數f（x）=cos（πx+φ）（0＜φ＜π2）的部分圖象如圖所示，若方程f（x）=a在（0，x0）上有兩個不同的實數解x1，x2，則x1f（x1）+x2f（x2）的取值范圍是（ ）

7．已知數列{an}的通項公式是an=n2sin（2n+12π），則a1+a2+a3+…+a12=（ ）

四、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟

22．已知函數f（x）=x-1x-alnx（a∈R）．（1）若函數f（x）在（2，+∞）上單調遞增，求a的取值范圍；（2）若函數f（x）有兩個不同的極值點x1，x2（x1＞x2），不等式f（x1）＜mx2恒成立，求實數m的取值范圍．

1．命題“?x∈R，x²-x+1=0”的否定為（　　）

2．無字證明是指禁用圖象而無需文字解釋就能不證自明的數學命題，由于其不證自明的特性，這種證明方式被認為比嚴格的數學證明更為優雅與條理，如圖，請寫出該圖驗證的不等式（　　）

5．如圖，從高為h的氣球（A）上測量待建規劃鐵橋（BC）的長，如果測得橋頭（B）的俯角是α，橋頭（C）的俯角是β，則橋BC的長為（　　）

6．函數f（x）=cos（πx+φ）（0＜φ＜
π
2
）的部分圖象如圖所示，若方程f（x）=a在（0，x₀）上有兩個不同的實數解x₁，x₂，則x₁f（x₁）+x₂f（x₂）的取值范圍是（　　）

7．已知數列{a_n}的通項公式是
a
n
=
n
2
sin
（
2
n
+
1
2
π
）
，則a₁+a₂+a₃+…+a₁₂=（　　）

22．已知函數
f
（
x
）
=
x
-
1
x
-
alnx
（
a
∈
R
）
．
（1）若函數f（x）在（2，+∞）上單調遞增，求a的取值范圍；
（2）若函數f（x）有兩個不同的極值點x₁，x₂（x₁＞x₂），不等式f（x₁）＜mx₂恒成立，求實數m的取值范圍．