2022-2023學年吉林省長春104中九年級（上）期末數(shù)學試卷

一、選擇題（本大題共8小題，每小題3分，共24分）

• 1．使代數(shù)式

  x

  -

  1

  有意義的x的取值范圍是（　　）

  A．x≥-1

  B．x＞-1

  C．x≥1

  D．x＞1
  組卷：1724引用：11難度：0.9

  解析

• 2．若△ABC∽△DEF，相似比為2：1，則△ABC與△DEF的周長的比為（　　）

  A．2：1

  B．4：1

  C．8：1

  D．16：1
  組卷：185引用：1難度：0.8

  解析

• 3．某校為了了解550名九年級學生的視力情況，從中抽取了70名學生進行測試，下列說法正確的是（　　）

  A．總體是550	B．樣本容量是70
  C．樣本是70名學生	D．個體是每個學生
  組卷：108引用：2難度：0.7

  解析

• 4．一元二次方程x²+2x+1=0的根的情況是（　　）

  A．無法判斷	B．有兩個相等的實數(shù)根
  C．有兩個不相等的實數(shù)根	D．沒有實數(shù)根
  組卷：65引用：6難度：0.7

  解析

• 5．如圖，在坡角為α的山坡上栽樹，要求相鄰兩樹之間的水平距離為6米，那么相鄰兩樹在坡面上的距離AB為（　　）

  A．6cosα

  B． 6 cosα

  C．6sinα

  D． 6 sinα
  組卷：342引用：6難度：0.6

  解析

• 6．在平面直角坐標系中，將拋物線y=x²-4先向右平移2個單位，再向上平移2個單位，得到的拋物線的表達式是（　　）

  A．y=（x-2）2-2

  B．y=（x+2）2+2

  C．y=（x-2）2+2

  D．y=（x+2）2-2
  組卷：281引用：11難度：0.7

  解析

• 7．如圖，AB是⊙O的直徑，點C、D在⊙O上．若∠BAC=30°．則∠ADC的大小是（　　）

  A．130°

  B．120°

  C．110°

  D．100°
  組卷：1050引用：11難度：0.7

  解析

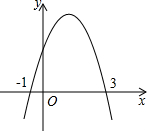• 8．已知二次函數(shù)y=ax²+bx+c（a≠0）的圖象如圖所示，以下四個結論：
  ①a＜0
  ②該函數(shù)的圖象關于直線x=1對稱
  ③b²-4ac＜0
  ④4a-2b+c＞0
  其中正確結論的個數(shù)是（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：250引用：2難度：0.7

  解析

三、解答題（本大題共10小題，共78分）

• 23．如圖，在△ABC中，AB=10，AC=6，BC=8，點P從點A出發(fā)，以每秒5個單位的速度沿AC向終點C勻速運動．當點P不與點A、C重合時，過點P作PQ⊥AB交AB于點Q，以PQ為邊向上作正方形PQMN，設正方形PQMN與△ABC重疊部分面積為S（平方單位），點P的運動時間為t（秒）．
  （1）用含t的代數(shù)式表示線段PQ的長度為

  ；
  （2）當點N落在線段BC上時，求t的值；
  （3）求S與t之間的函數(shù)關系式；
  （4）當點N恰好落在△ABC的角平分線上時，直接寫出t的值．
  組卷：99引用：1難度：0.2

  解析

• 24．在平面直角坐標系中，已知拋物線y=x²-2ax+a²+4a（a為常數(shù)）．
  （1）當拋物線經過（1，4）時，求a的值．
  （2）該拋物線的頂點坐標為

  （用含a的代數(shù)式表示）．
  （3）當a=1時，若-1≤x≤m時，4≤y≤8，則m的取值范圍是

  ．
  （4）當x≤2a時，若函數(shù)y=x²-2ax+a²+4a（a為常數(shù)）的圖象的最低點到直線y=1的距離為2，求a的值．
  組卷：311引用：1難度：0.5

  解析