2022-2023學(xué)年廣東省廣州六中、二中、廣雅、省實(shí)、執(zhí)信五校聯(lián)考高一（下）期末數(shù)學(xué)試卷

一、單項(xiàng)選擇題：本大題共8小題，每小題5分，共40分，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的，請把正確選項(xiàng)在答題卡中的相應(yīng)位置涂黑．

• 1．已知復(fù)數(shù)

  z

  =

  1

  -

  2

  i

  1

  +

  i

  （i是虛數(shù)單位），則

  z

  對應(yīng)的點(diǎn)在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：94引用：2難度：0.7

  解析

• 2．已知平面向量

  a

  與

  b

  為單位向量，它們的夾角為

  π

  3

  ，則|

  2

  a

  +

  b

  |=（　　）

  A． 2

  B． 3

  C． 5

  D． 7
  組卷：311引用：6難度：0.8

  解析

• 3．已知函數(shù)

  f

  （

  x

  ）

  =

  1 x ， x ＞ 0

  x + 2 ， x ≤ 0

  ，則方程f（x）-3^|x|=0的解的個(gè)數(shù)是（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：1040引用：3難度：0.8

  解析

• 4．函數(shù)y=sin（x+

  π

  3

  ）sin（x+

  π

  2

  ）的最小正周期是（　　）

  A． π 4

  B． π 2

  C．π

  D．2π
  組卷：250引用：3難度：0.6

  解析

• 5．下列不等式恒成立的是（　　）

  A． b a + a b ≥ 2

  B． ab ≥ （ a + b 2 ） 2

  C． a + b ≥ 2 | ab |

  D．a(chǎn)2+b2≥-2ab
  組卷：1629引用：4難度：0.8

  解析

• 6．已知a,b是兩條不重合的直線，α，β，γ是三個(gè)不重合的平面，則下列命題正確的是（　　）

  A．若a∥α，β∥α，則a∥β	B．若α⊥β，a⊥β，則a∥α
  C．若α⊥γ，β⊥γ，則α∥β	D．若a∥α，b⊥α，則a⊥b
  組卷：293引用：5難度：0.7

  解析

• 7．北斗三號全球衛(wèi)星導(dǎo)航系統(tǒng)是我國航天事業(yè)的重要成果．在衛(wèi)星導(dǎo)航系統(tǒng)中，地球靜止同步衛(wèi)星的軌道位于地球赤道所在平面，軌道高度（軌道高度是指衛(wèi)星到地球表面的距離）為h.將地球看作是一個(gè)球心為O，半徑為r的球，其上點(diǎn)A的緯度是指OA與赤道平面所成角的度數(shù)．如果地球表面上某一觀測點(diǎn)與該衛(wèi)星在同一條子午線（經(jīng)線）所在的平面，且在該觀測點(diǎn)能直接觀測到該衛(wèi)星．若該觀測點(diǎn)的緯度值為a,觀測該衛(wèi)星的仰角為β，則下列關(guān)系一定成立的是（　　）

  A． r + h cosβ = r cos （ α + β ）	B． h cosβ = r cos （ α + β ）
  C． r + h sinβ = r sin （ α + β ）	D． h sinβ = r sin （ α + β ）
  組卷：264引用：7難度：0.5

  解析

四、解答題：本大題共6小題，第17題10分，18、19、20、21、22題各12分，共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟．必須把解答過程寫在答題卡相應(yīng)題號指定的區(qū)域內(nèi)，超出指定區(qū)域的答案無效

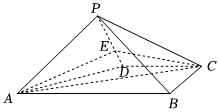• 21．如圖，已知四棱錐P-ABCD的底面ABCD為梯形，AB∥CD，PA=PD=PB，BC=CD=1，AB=2，∠BCD=

  π

  3

  ，直線PA與底面ABCD所成角為

  π

  4

  ．
  （1）若E為PD上一點(diǎn)且PE=2ED，證明：PB∥平面ACE；
  （2）求二面角P-AD-B的余弦值．
  組卷：286引用：1難度：0.5

  解析

• 22．設(shè)a為正數(shù)，函數(shù)f（x）=ax²+bx+c滿足f（0）=1且f（x）=f

  （

  2

  a

  -

  x

  ）

  ．
  （1）若f（1）=1，求f（x）；
  （2）設(shè)g（x）=log₂（x-2

  x

  +2），若對任意實(shí)數(shù)t,總存在x₁，x₂∈[t-1，t+1]，使得f（x₁）-f（x₂）≥g（x₃）-g（x₄）對所有x₃，x₄∈

  [

  1

  4

  ，

  4

  ]

  都成立，求a的取值范圍．
  組卷：262引用：2難度：0.2

  解析