2022-2023學年上海實驗學校高二（下）期中數學試卷

一.填空題（每題4分，共40分）

• 1．過點P（2，3），且一個法向量為

  n

  =

  （

  3

  ，-

  1

  ）

  的直線的點法式方程是

  ．
  組卷：124引用：1難度：0.7

  解析

• 2．若x²+y²-2x-4y=0，求圓心坐標為

  ．
  組卷：1751引用：6難度：0.9

  解析

• 3．橢圓

  x

  2

  2

  +

  y

  2

  4

  =1的焦距是

  ．
  組卷：164引用：4難度：0.8

  解析

• 4．雙曲線

  x

  2

  -

  y

  2

  3

  =

  1

  的漸近線的夾角為

  ．
  組卷：62引用：3難度：0.9

  解析

• 5．已知直線l：ax+（2a-1）y+a-3=0，當a變化時，直線l總是經過定點，則定點坐標為

  ．
  組卷：200引用：3難度：0.8

  解析

• 6．若原點到直線l：ax+y+8=0距離為4，則a的值是

  ．
  組卷：245引用：1難度：0.9

  解析

四.附加題（共20分）

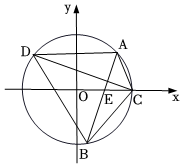• 19．如圖，過點E（1，0）的直線與圓O：x²+y²=4相交于A，B兩點，過點C（2，0）且與AB垂直的直線與圓O的另一交點為D．
  （1）當點B坐標為（0，-2）時，求直線CD的方程；
  （2）記點A關于x軸的對稱點為F（異于點A，B），求證：直線BF恒過定點；
  （3）求四邊形ACBD面積S的取值范圍．
  組卷：159引用：2難度：0.6

  解析

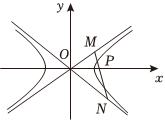• 20．如圖，已知雙曲線C的方程為

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  ，兩條漸近線的夾角的余弦值為

  3

  5

  ，焦點到漸近線的距離為1，M、N兩動點在雙曲線C的兩條漸近線上，且分別位于第一象限和第四象限，P是直線MN與雙曲線右支的一個公共點，

  MP

  =

  λ

  PN

  ．
  （1）求雙曲線C的方程；
  （2）當λ=1時，求

  PM

  ?

  PN

  的取值范圍；
  （3）試用λ表示△MON的面積S，設雙曲線C上的點到其焦點的距離的取值范圍為集合Ω，若

  λ

  5

  ∈

  Ω

  ，求S的取值范圍．
  組卷：40引用：1難度：0.6

  解析