2022-2023學年重慶十八中九年級（上）期末數學試卷

一.選擇題（每題4分，共12小題）

• 1．在如圖所示標志中，既是軸對稱圖形，又是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：2233引用：33難度：0.8

  解析

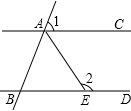• 2．如圖，AC∥BD，AE平分∠BAC交BD于點E，若∠1=66°，則∠2=（　　）

  A．123°

  B．128°

  C．132°

  D．142°
  組卷：689引用：8難度：0.8

  解析

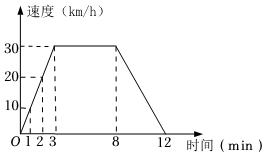• 3．一輛汽車行駛的速度（km/h）與時間（min）之間的變化關系如圖所示，說法正確的是（　　）

  A．時間是因變量，速度是自變量

  B．汽車在1～3min時勻速行駛

  C．汽車在3～8min時勻速行駛

  D．汽車最快的速度是10km/h
  組卷：1609引用：8難度：0.5

  解析

• 4．以下命題正確的是（　　）

  A．鄰邊相等的平行四邊形是矩形

  B．三角形的外角等于兩個內角的和

  C．對角線互相垂直的平行四邊形是菱形

  D．對角線互相平分且相等的四邊形是菱形
  組卷：68引用：2難度：0.6

  解析

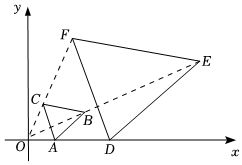• 5．如圖，在平面直角坐標系中，已知A（1，0），B（2，1），D（3，0），△ABC與△DEF位似，原點O是位似中心，則E點的坐標是（　　）

  A．（7，4）

  B．（7，3）

  C．（6，4）

  D．（6，3）
  組卷：2182引用：18難度：0.6

  解析

• 6．如果m=2

  10

  -1，那么m的取值范圍是（　　）

  A．4＜m＜5

  B．4＜m＜6

  C．5＜m＜6

  D．5＜m＜7
  組卷：135引用：1難度：0.7

  解析

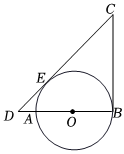• 7．如圖，AB是⊙O的直徑，點D在BA的延長線上，

  2

  OB

  =

  OD

  ，DC與⊙O相切于點E，BC與⊙O相切于點B交DE的延長線于點C，若⊙O的半徑為1，EC的長是（　　）

  A． 2 + 1

  B． 2 2

  C． 2 + 2

  D． 2 2 + 1
  組卷：501引用：2難度：0.6

  解析

• 8．端午節又稱端陽節，是中華民族重要的傳統節日，我國各地都有吃粽子的習俗．某超市以10元每袋的價格購進一批粽子，根據市場調查，售價定為每袋16元，每天可售出200袋；若售價每降低1元，則可多售出80袋，問此種粽子售價降低多少元時，超市每天售出此種粽子的利潤可達到1440元？若設每袋粽子售價降低x元，則可列方程為（　　）

  A．（16-x-10）（200+80x）=1440

  B．（16-x）（200+80x）=1440

  C．（16-x-10）（200-80x）=1440

  D．（16-x）（200-80x）=1440
  組卷：798引用：10難度：0.8

  解析

三.解答題（17、18每題8分，19-25每題10分）

• 24．如圖1，拋物線y=ax²+bx+3（a≠0）與x軸正半軸交于點A，B，與y軸正半軸交于點C，且OC=OB=3OA，點D為拋物線的頂點．
  
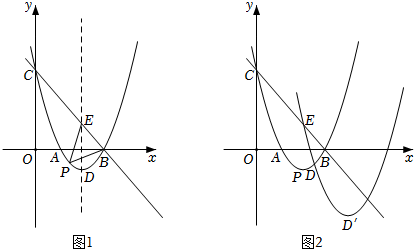
  （1）求該拋物線的函數表達式；
  （2）點P為直線BC下方該拋物線上任意一點，點E為直線BC與該拋物線對稱軸的交點，求△PBE面積的最大值；
  （3）如圖2，將該拋物線沿射線CB的方向平移2

  2

  個單位后得到新拋物線y'，新拋物線y′的頂點為D'，過（2）問中使得△PBE面積為最大時的點P作平行于y軸的直線交新拋物線y'于點M．在新拋物線y′的對稱軸上是否存在點N，使得以點P，D'，M，N為頂點的四邊形是平行四邊形？若存在，請直接寫出點N的坐標；若不存在，請說明理由．
  組卷：582引用：2難度：0.3

  解析

• 25．如圖，在△ABC中，∠BAC=90°，AB=AC．
  
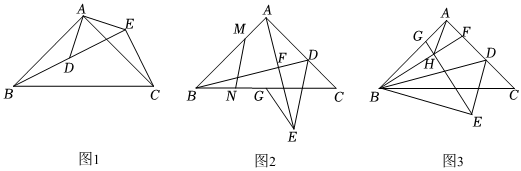
  （1）如圖1，點D為△ABC內一點，連接AD，過點A作AE⊥AD，AD=AE，連接DE，BD，CE，已知AB=

  5

  ，AD=1，當B、D、E三點共線時，求ABCE的面積；
  （2）如圖2，在AC上取點D，連接BD，過點A作AE⊥BD于點F，AE=BD，取BC中點G，連接GE，ED，在AB上取點M，過點M作MN∥DE交BC于點N，MN=GE，求證：BN=DC；
  （3）如圖3，在AC上取點D，連接BD，將△ABD沿BD翻折至ABDE處，在AC上取點F，連接BF，過點E作EH⊥BF于點F，GE交BF于點H，連接AH，若GE：BF=

  3

  ：2，AB=2

  2

  ，求AH的最小值．
  組卷：699引用：2難度：0.9

  解析