2023-2024學年陜西省西安市雁塔區高新一中九年級（上）第一次月考數學試卷

一、選擇題(共10小題，每題3分)

• 1．已知點A（3，-2）在雙曲線y=

  k

  x

  上，則下列各點也在此雙曲線上的是（　　）

  A．（1，6）

  B．（2，3）

  C．（-1，-6）

  D．（-2，3）
  組卷：577引用：5難度：0.9

  解析

• 2．已知四條線段a,b,c,d是成比例線段，其中b=3cm,c=4cm,d=6cm,則線段a的長度為（　　）

  A．8cm

  B．2cm

  C．4cm

  D．1cm
  組卷：633引用：7難度：0.8

  解析

• 3．一張正方形紙片在太陽光下的影子不可能是（　　）

  A．平行四邊形

  B．矩形

  C．梯形

  D．線段
  組卷：363引用：9難度：0.5

  解析

• 4．一個口袋中有紅球、白球共20個，這些球除顏色外都相同．將口袋中的球攪拌均勻，從中隨機摸出一個球，記下它的顏色后再放回口袋中，不斷重復這一過程，共摸了100次球，發現有40次摸到白球．請你估計這個口袋中有（　　）個白球．

  A．12

  B．8

  C．6

  D．4
  組卷：266引用：3難度：0.6

  解析

• 5．已知點A（x₁，y₁），B（x₂，y₂），C（x₃，y₃）都在反比例函數y=

  a

  2

  +

  1

  x

  （a是常數）的圖象上，且y₁＜y₂＜0＜y₃，則x₁，x₂，x₃的大小關系為（　　）

  A．x2＞x1＞x3

  B．x1＞x2＞x3

  C．x3＞x2＞x1

  D．x3＞x1＞x2
  組卷：3310引用：24難度：0.7

  解析

• 6．如圖，小明晚上由路燈A下的點B處走到點C處時，測得自身影子CD的長為1米，他繼續往前走3米到達點E處（即CE=3米），測得自己影子EF的長為2米，已知小明的身高是1.5米，那么路燈A的高度AB是（　　）

  A．4.5米

  B．6米

  C．7.2米

  D．8米
  組卷：1697引用：13難度：0.7

  解析

• 7．用圖中兩個可以自由轉動的轉盤做“配紫色”游戲，分別旋轉兩個轉盤，若其中一個轉盤轉出紅色，另一個轉盤轉出藍色即可配成紫色．那么可配成紫色的概率是（　　）

  A． 2 9

  B． 1 2

  C． 5 9

  D． 2 3
  組卷：315引用：6難度：0.6

  解析

• 8．如圖，已知正方形ABCD，點E為BC的中點，連接ED交AC于F，則S_△DFC：S_{四邊形ABEF}的值為（　　）

  A． 1 4

  B． 2 5

  C． 7 13

  D． 3 8
  組卷：848引用：8難度：0.6

  解析

三、解答題（共8小題，共69題）

• 24．已知，矩形OCBA在平面直角坐標系中的位置如圖所示，點C在x軸的正半軸上，點A在y軸的正半軸上，已知點B的坐標為（4，2），反比例函數y=

  k

  x

  的圖象經過AB的中點D，且與BC交于點E，設直線DE的解析式為y=mx+n,連接OD，OE．
  （1）求反比例函數y=

  k

  x

  的表達式和點E的坐標；
  （2）點M為y軸正半軸上一點，若△MBO的面積等于△ODE的面積，求點M的坐標；
  （3）點P為x軸上一點，點Q為反比例函數y=

  k

  x

  圖象上一點，是否存在點P、Q使得以點P，Q，D，E為頂點的四邊形為平行四邊形？若存在，直接寫出點Q的坐標；若不存在，請說明理由．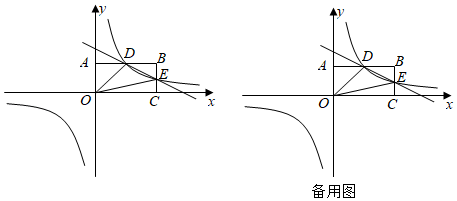
  
  組卷：781引用：3難度：0.3

  解析

• 25．問題初探：
  （1）如圖1，已知△ABC與△DEF都是等腰三角形，頂角∠ACB=∠EDF=90°，且AB、EF的中點均為O．請寫出BF與CD間的數量關系，并證明；
  問題深入：
  （2）如圖2，已知△ABC與△DEF都是等邊三角形，AB、EF的中點均為O，請寫出BF與CD間的數量關系，并證明；
  ?
  拓展創新：
  （3）如圖3，在Rt△ABC和Rt△DEC中，∠ACB=∠DCE=90°，BC=2AC，EC=2DC，點E在△ABC內部，直線AD與BE交于點F，直接寫出線段AF，BF，CF之間的數量關系

  ．
  組卷：181引用：1難度：0.5

  解析