試卷征集
          
                
          
            
          
            
          
                
          
                    
                    
          加入會員
          
                
          
            
          
            
          
                
          
                    
                    
          操作視頻
          
                
          
            
          
        
          
    
          

    
          
        
    
          
    
          
    
          
        
          
            



          
    當前位置：
    試卷中心
    >
    試卷詳情

          


          
    
          
        
          
            2010年廣東省東莞市清溪中學初三數學競賽試卷
        
          
        
          
            發布：2024/11/10 11:30:2
        
          
            
          一、選擇題（每小題5分，共50分）
          
            
            
                    
          • 
                        
            1．設a、b、c滿足abc≠0，且a+b=c,則
            b
            2
            +
            c
            2
            -
            a
            2
            2
            bc
            +
            c
            2
            +
            a
            2
            -
            b
            2
            2
            ca
            +
            a
            2
            +
            b
            2
            -
            c
            2
            2
            ab
            的值為（　　）
            組卷：756引用：6難度：0.9
            
                    
            • 
                    
          • 
                        
            2．已知a是非零實數，則
            a
            |
            a
            |
            +
            a
            2
            |
            a
            2
            |
            +
            a
            3
            |
            a
            3
            |
            的值是（　　）
            組卷：161引用：2難度：0.9
            
                    
            • 
                    
          • 
                        
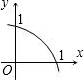            3．二次函數y=ax2+bx+c的圖象的一部分如圖，則a的取值范圍是（　　）
            組卷：138引用：4難度：0.9
            
                    
            • 
                    
          • 
                        
            4．不等式0≤ax+5≤4的整數解是1，2，3，4，則a的取值范圍是（　　）
            組卷：1912引用：10難度：0.9
            
                    
            • 
                    
          • 
                        
            5．若三角形的三邊長度均為整數，其中兩邊長的差是7，且三角形的周長是奇數，則第三邊長可能是（　　）
            組卷：104引用：2難度：0.9
            
                    
            • 
            
          
        
            
          二、填空題（每小題10分，共50分）
          
            
            
                    
          • 
                        
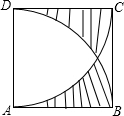            14．如圖，正方形ABCD的邊AB=1，
            ?
            BD
            和
            ?
            AC
            都是以1為半徑的圓弧，則無陰影部分的兩部分的面積之差是 
            ．
            組卷：318引用：5難度：0.7
            
                    
            • 
                    
          • 
                        
            15．如果記
            y
            =
            x
            2
            1
            +
            x
            2
            =
            f
            （
            x
            ）
            ，并且f（1）表示x=1時y的值，即
            f
            （
            1
            ）
            =
            1
            1
            +
            1
            =
            1
            2
            ，
            f
            （
            1
            2
            ）
            表示
            x
            =
            1
            2
            時y的值，即
            f
            （
            1
            2
            ）
            =
            1
            2
            1
            +
            （
            1
            2
            ）
            2
            =
            1
            5
            ，那么
            f
            （
            1
            ）
            +
            f
            （
            2
            ）
            +
            f
            （
            1
            2
            ）
            +
            f
            （
            3
            ）
            +
            f
            （
            1
            3
            ）
            +
            …
            +
            f
            （
            n
            ）
            +
            f
            （
            1
            n
            ）
            =
             

            （結果用含n的代數式表示，n為正整數．）
            組卷：364引用：2難度：0.5
            
                    
            • 
            
          
    
          

    

          


        
          
    
          
    
          
         
          APP開發者：深圳市菁優智慧教育股份有限公司| 應用名稱：菁優網 | 應用版本：5.0.7 |隱私協議|第三方SDK|用戶服務條款
          本網部分資源來源于會員上傳，除本網組織的資源外，版權歸原作者所有，如有侵犯版權，請立刻和本網聯系并提供證據，本網將在三個工作日內改正