2023年湖北省隨州市曾都區(qū)中考數(shù)學(xué)一模試卷
發(fā)布：2024/5/22 8:0:8
一、選擇題（本題共10小題，每小題3分，共30分．每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的）
-
1．2023的相反數(shù)是（ ）
組卷：5349引用：291難度：0.8 -
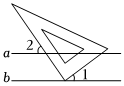2．如圖，已知直線a∥b,把三角尺的直角頂點(diǎn)放在直線b上，若∠1=36°，則∠2的度數(shù)為（ ）組卷：36引用：1難度：0.6 -
3．《全國(guó)國(guó)土空間規(guī)劃綱要（2021—2035年）》明確18.65億畝耕地目標(biāo)任務(wù)要保持到2035年不變．?dāng)?shù)據(jù)“18.65億”用科學(xué)記數(shù)法表示為（ ）
組卷：58引用：1難度：0.8 -
4．不等式組
的解集在數(shù)軸上表示正確的是（ ）x+1≥0，x-1＜0組卷：654引用：11難度：0.7 -
5．下列幾何體中，無(wú)論怎樣放置在平面上，其三視圖都是全等形的是（ ）
組卷：13引用：1難度：0.8 -
6．一個(gè)布袋中放著6個(gè)黑球和12個(gè)紅球，除了顏色以外沒(méi)有任何其他區(qū)別，則從布袋中任取1個(gè)球，取出紅球的概率是（ ）
組卷：144引用：1難度：0.8 -
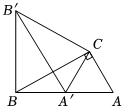7．如圖，在△ABC中，∠ACB=90°，AC=1，將△ABC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)60°至△A′B′C，點(diǎn)A的對(duì)應(yīng)點(diǎn)A′恰好落在AB上，則BB′的長(zhǎng)為（ ）組卷：156引用：2難度：0.6 -
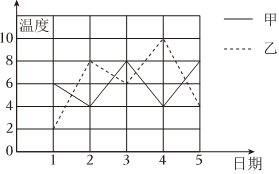8．甲、乙兩地今年4月份前5天的日最低氣溫如圖所示，則下列描述正確的是（ ）組卷：76引用：1難度：0.8
三、解答題（本題共8小題，共72分．解答應(yīng)寫(xiě)出必要的演算步驟、文字說(shuō)明或證明過(guò)程）
-
23．【問(wèn)題提出】如圖1，在Rt△ABC中，∠ACB=90°，點(diǎn)E，F(xiàn)分別為邊AC，BC的中點(diǎn)，將△EFC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)α（0°＜α＜360°），連接AE，BF，試探究AE，BF之間存在怎樣的數(shù)量關(guān)系和位置關(guān)系？
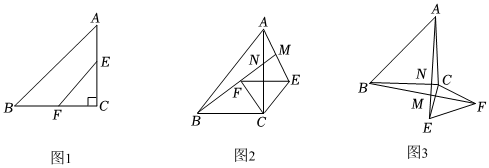
【特例探究】若AC=BC，將△EFC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)至圖2的位置，直線BF與AE，AC分別交于點(diǎn)M，N．按以下思路完成填空（第一個(gè)空填推理依據(jù)，第二個(gè)空填數(shù)量關(guān)系，第三個(gè)空填位置關(guān)系）：
∵AC=BC，點(diǎn)E，F(xiàn)分別為邊AC，BC的中點(diǎn)，
∴CE=CF．
∵∠ACB=∠ECF，
∴∠ACE=∠BCF．
∴△ACE≌△BCF（ ）．
∴AE BF，∠CAE=∠CBF．
又∵∠ANM=∠BNC，
∴∠AMN=∠BCN=90°．
∴AE BM．
【猜想證明】若BC=nAC（n＞1），△EFC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)至圖3的位置，直線AE與BF，BC分別交于點(diǎn)M，N，猜想AE與BF之間的數(shù)量關(guān)系與位置關(guān)系，并就圖3所示的情況加以證明；
【拓展運(yùn)用】若AC=4，BC=6，將△EFC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)α（0°＜α＜360°），直線AE與BF相交于點(diǎn)M，當(dāng)以點(diǎn)C，E，M，F(xiàn)為頂點(diǎn)的四邊形是矩形時(shí)，請(qǐng)直接寫(xiě)出BM的長(zhǎng)．組卷：55引用：3難度：0.5 -
24．已知拋物線y=ax2+bx-6（a≠0）與x軸交于點(diǎn)A（-2，0），點(diǎn)B（6，0），與y軸交于點(diǎn)C．
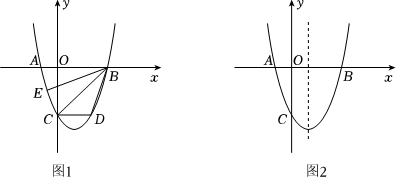
（1）求拋物線的解析式；
（2）如圖1，過(guò)點(diǎn)C作CD∥x軸交拋物線于點(diǎn)D，點(diǎn)E是y軸左側(cè)拋物線上一點(diǎn)，若BC恰好平分∠DBE，求直線BE的解析式；
（3）如圖2，點(diǎn)P是拋物線對(duì)稱(chēng)軸上的一點(diǎn)，在拋物線上是否存在點(diǎn)M，使△PMB是以PM為斜邊的等腰直角三角形，若存在，請(qǐng)直接寫(xiě)出所有點(diǎn)M的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由．組卷：149引用：1難度：0.1