2023-2024學年河南省鄭州四中九年級（上）第一次學習比賽數學試卷

一.選擇題（每小題3分，共30分）

• 1．下列關于x的方程中，一定是一元二次方程的是（　　）

  A．x-1=0

  B．x3+x=3

  C．x2+3x-5=0

  D．ax2+bx+c=0
  組卷：1382引用：31難度：0.9

  解析

• 2．下列條件中，能判定平行四邊形是菱形的是（　　）

  A．對角線互相垂直	B．對角線相等
  C．對角線互相平分	D．有一個角是直角
  組卷：328引用：6難度：0.5

  解析

• 3．要檢驗一個四邊形畫框是否為矩形，可行的測量方法是（　　）

  A．測量四邊形畫框的兩個角是否為90°

  B．測量四邊形畫框的對角線是否相等且互相平分

  C．測量四邊形畫框的一組對邊是否平行且相等

  D．測量四邊形畫框的四邊是否相等
  組卷：1645引用：8難度：0.5

  解析

• 4．已知關于x的一元二次方程x²+kx-2=0有一個根是-2，則另一個根是（　　）

  A．1

  B．-1

  C．2

  D．-2
  組卷：460引用：11難度：0.7

  解析

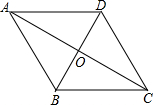• 5．如圖，四邊形ABCD的兩條對角線相交于點O，且互相平分．添加下列條件，仍不能判定四邊形ABCD為菱形的是（　　）

  A．AC⊥BD

  B．AB=AD

  C．AC=BD

  D．∠ABD=∠CBD
  組卷：3075引用：35難度：0.5

  解析

• 6．若方程x²+2x+m+1=0有兩個不相等的實數根，則m的值可以是（　　）

  A．-1

  B．0

  C．1

  D． 2
  組卷：211引用：6難度：0.7

  解析

• 7．根據下表：
  

  x	-3	-2	-1	…	4	5	6
  x2-bx-5	13	5	-1	…	-1	5	13

  確定方程x²-bx-5=0的解的取值范圍是（　　）

  A．-2＜x＜-1或4＜x＜5	B．-2＜x＜-1或5＜x＜6
  C．-3＜x＜-2或5＜x＜6	D．-3＜x＜-2或4＜x＜5
  組卷：825引用：22難度：0.6

  解析

三、解答題（共8小題，共75分）

• 22．閱讀材料，解決問題．
  相傳古希臘畢達哥拉斯學派的數學家經常在沙灘上研究數學問題．他們在沙灘上畫點或用小石子來表示數，比如，他們研究過1、3、6、10…，由于這些數可以用圖中所示的三角點陣表示，他們就將每個三角點陣中所有的點數和稱為三角數．
  
  則第n個三角數可以用1+2+3+…+（n-2）+（n-1）+n=

  n

  （

  n

  +

  1

  ）

  2

  （n≥1且為整數）來表示．
  （1）若三角數是55，則n=

  ；
  （2）把第n個三角點陣中各行的點數依次換為2，4，6，…，2n,…，請用含n的式子表示前n行所有點數的和；
  （3）在（2）中的三角點陣中前n行的點數的和能為120嗎？如果能，求出n,如果不能，請說明理由．
  組卷：122引用：4難度：0.4

  解析

• 23．綜合與實踐課上，老師讓同學們以“正方形的折疊”為主題開展數學活動．
  （1）操作判斷
  操作一：對折正方形紙片，使AD與BC重合，得到折痕EF，把紙片展平；
  操作二：在BE上選一點H，沿CH折疊，使點B落在EF上的點G處，得到折痕CH，把紙片展平；根據以上操作，直接寫出圖1中∠CHB的度數：

  ．
  （2）拓展應用
  小華在以上操作的基礎上，繼續探究，延長HG交AD于點M，連接CM交EF于點N（如圖2）．判斷△MGN的形狀，并說明理由．
  （3）遷移探究
  如圖3，已知正方形ABCD的邊長為6cm,當點H是邊AB的三等分點時，把△BCH沿CH翻折得△GCH，延長HG交AD于點M，請直接寫出AM的長．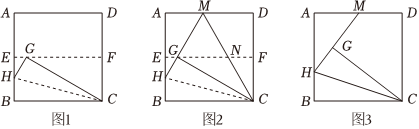
  
  組卷：830引用：3難度：0.5

  解析