2023-2024學年重慶市南岸區茶園新城中學九年級（上）月考數學試卷（10月份）

一、選擇題（每小題4分，共40分）

• 1．小紅有三頂帽子，分別為白色、紅色和粉色，有兩條圍巾，分別為白色和紅色．她隨機拿出一頂帽子和一條圍巾戴上，恰好為紅色帽子和紅色圍巾的概率是（　　）

  A． 1 3

  B． 1 2

  C． 1 6

  D． 5 6
  組卷：349引用：4難度：0.5

  解析

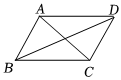• 2．如圖，要使平行四邊形ABCD成為矩形，需要添加的條件是（　　）

  A．∠ABD=∠CBD

  B．∠ABC=90°

  C．AC⊥BD

  D．AB=BC
  組卷：1395引用：10難度：0.9

  解析

• 3．一元二次方程2x²-3x+1=0根的情況是（　　）

  A．沒有實數根	B．有兩個相等的實數根
  C．有兩個不相等的實數根	D．無法確定
  組卷：947引用：15難度：0.7

  解析

• 4．在一個不透明的盒子里裝有若干個白球和15個紅球，這些球除顏色不同外其余均相同，每次從袋子中摸出一個球記錄下顏色后再放回，經過多次重復試驗，發現摸到白球的頻率穩定在0.4左右，則袋中白球約有（　　）

  A．5個

  B．10個

  C．15個

  D．25個
  組卷：1404引用：21難度：0.9

  解析

• 5．一元二次方程x²-6x-5=0配方可變形為（　　）

  A．（x-3）2=14

  B．（x-3）2=4

  C．（x+3）2=14

  D．（x+3）2=4
  組卷：616引用：16難度：0.7

  解析

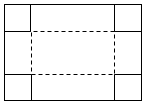• 6．如圖，把一塊長為45cm,寬為25cm的矩形硬紙板的四角剪去四個相同的小正方形，然后把紙板沿虛線折起，做成一個無蓋紙盒．若該無蓋紙盒的底面積為625cm²，設剪去小正方形的邊長為x cm,則可列方程為（　　）

  A．（45-2x）（25-x）=625	B．（45-x）（25-x）=625
  C．（45-x）（25-2x）=625	D．（45-2x）（25-2x）=625
  組卷：364引用：4難度：0.8

  解析

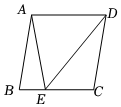• 7．如圖，已知E是菱形ABCD的邊BC上一點，且∠DAE=∠B=80°，那么∠CDE的度數為（　　）

  A．35°

  B．30°

  C．25°

  D．20°
  組卷：943引用：4難度：0.6

  解析

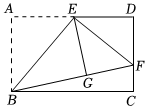• 8．如圖，矩形ABCD中，E是AD的中點，將△ABE沿直線BE折疊后得到△GBE，延長BG交CD于點F，若AB=3，

  BC

  =

  2

  5

  ，則FD的長為（　　）

  A．1

  B．2

  C． 5 3

  D． 3 3
  組卷：230引用：3難度：0.6

  解析

三、解答題（19題8分，其余各題每題10分，共78分）

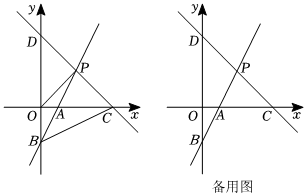• 25．如圖，在平面直角坐標系中，直線y=2x-2與x軸、y軸分別交于點A、點B，與直線CD：y=kx+b（k≠0）交于點P，OC=OD=4OA．
  （1）求直線CD的解析式；
  （2）連接OP、BC，若直線AB上存在一點Q，使得S_△PQC=S_{四邊形OBCP}，求點Q的坐標；
  （3）將直線CD向下平移1個單位長度得到直線，直線l與x軸交于點E，點N為直線l上的一點，在平面直角坐標系中，是否存在點M，使以點O，E，N，M為頂點的四邊形是矩形？若存在，請直接寫出點M的坐標；若不存在，請說明理由．
  組卷：1823引用：9難度：0.3

  解析

• 26．已知，在△ABC中，AC=BC，∠ACB=90°．
  （1）如圖1，點D、點E分別是線段AB上兩點，連接CD、CE，若AD=BE，且∠ECD=45°，求∠ECB的度數；
  （2）如圖2，點D、點E分別是線段AB上兩點，連接CD、CE，過點B作BF⊥AB交CE延長線于F，連接DF，若∠ECD=45°，求證：AD+BF=DF；
  （3）如圖3，M為射線AC上一點，N為射線CA上一點，且始終滿足CM=AN，過點C作MB的垂線交AB的延長線于點P，連接NP，猜想：NP、MB、CP之間的數量關系并證明你的結論．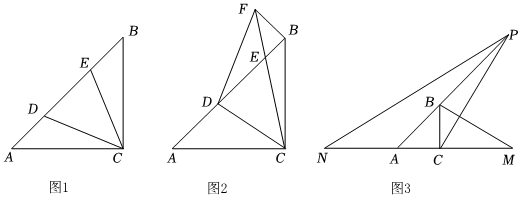
  
  組卷：918引用：5難度：0.3

  解析