2022年天津市寧河區蘆臺一中高考數學模擬試卷（一）

一、選擇題。（本題共9小題，每題5分，共45分）

• 1．已知集合A={x|y=lg（x²-x）}，B={x|1≤2^x≤4}，則A∪B=（　　）

  A．（1，2]	B．R
  C．（-∞，0）∪（1，2]	D．（-∞，2]
  組卷：200引用：3難度：0.7

  解析

• 2．已知向量

  a

  =（x,1），

  b

  =（4，x），則“x=2”是“

  a

  ∥

  b

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：253引用：10難度：0.9

  解析

• 3．已知函數

  f

  （

  x

  ）

  =

  2

  x

  3

  e

  x

  -

  1

  ，則f（x）的大致圖像為（　　）

  A．

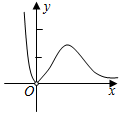
  B．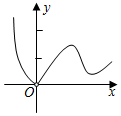

  C．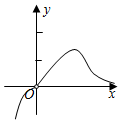

  D．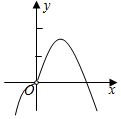
  組卷：219引用：3難度：0.7

  解析

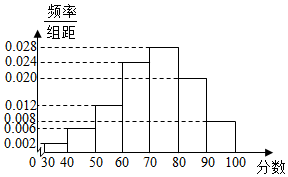• 4．某中學為了調查該校學生對于新冠肺炎防控的了解情況，組織了一次新冠肺炎防控知識競賽，并從該學校1500名參賽學生中隨機抽取了100名學生，并統計了這100名學生成績情況（滿分100分，其中80分及以上為優秀），得到了樣本頻率分布直方圖（如圖），根據頻率分布直方圖推測，這1500名學生中競賽成績為優秀的學生人數大約為（　　）

  A．360

  B．420

  C．480

  D．540
  組卷：349引用：3難度：0.9

  解析

• 5．已知函數f（x）=e^|x|+2x²．若a=f（0.6^0.7），b=f（log₂

  1

  3

  ），c=f（log₄5），則a,b,c的大小關系為（　　）

  A．a＜b＜c

  B．c＜b＜a

  C．a＜c＜b

  D．b＜c＜a
  組卷：413引用：3難度：0.7

  解析

• 6．設P，A，B，C為球O表面上的四個點，PA，PB，PC兩兩垂直，且PA=3，PB=6，三棱錐P-ABC的體積為18，則球O的體積為（　　）

  A． 23 46 3 π

  B． 343 6 π

  C． 27 6 π

  D． 243 2 π
  組卷：814引用：3難度：0.8

  解析

三、解答題。（本題共5題，共75分）

• 19．等差數列{a_n}的前n項和為S_n，數列{b_n}是等比數列，滿足a₁=3，b₁=1，b₂+S₂=10，a₅-2b₂=a₃．
  （1）求數列{a_n}和{b_n}的通項公式；
  （2）若數列{c_n}滿足c_2n-1=a_n，c_2n=（-1）ⁿa_nb_n，求數列{c_n}的前2n項和T_2n；
  （3）求

  n

  ∑

  k

  =

  1

  （

  -

  1

  ）

  k

  （

  6

  k

  +

  5

  ）

  b

  k

  a

  k

  a

  k

  +

  1

  ．
  組卷：839引用：4難度：0.4

  解析

• 20．已知函數f（x）=xlnx-

  a

  2

  x²+1．
  （1）若f（x）在（0，+∞）上單調遞減，求a的取值范圍；
  （2）若f（x）在x=1處的切線斜率是

  1

  2

  ，證明f（x）有兩個極值點x₁x₂，且3ln2＜|lnx₂-lnx₁|＜3．
  組卷：243引用：4難度：0.5

  解析