2022-2023學(xué)年四川省成都七中高二(下)入學(xué)數(shù)學(xué)試卷(理科)
發(fā)布:2024/8/9 8:0:9
一、選擇題:(本大題共12個小題,每小題5分,共60分,在每小題給出的選項中,只一項是符合要求的。)
-
1.拋物線x2=
y的準(zhǔn)線方程是( )14A.y=1 B.y=-1 C.y= 116D.y=- 116組卷:66引用:6難度:0.9 -
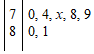 2.在一次數(shù)學(xué)測驗中,統(tǒng)計7名學(xué)生的成績分布莖葉圖如圖所示,若這7名學(xué)生的平均成績?yōu)?7分,則x的值為( )
2.在一次數(shù)學(xué)測驗中,統(tǒng)計7名學(xué)生的成績分布莖葉圖如圖所示,若這7名學(xué)生的平均成績?yōu)?7分,則x的值為( )A.5 B.6 C.7 D.8 組卷:17引用:7難度:0.9 -
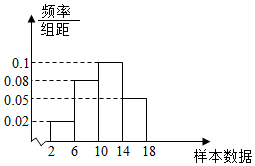 3.容量為100的樣本,其數(shù)據(jù)分布在[2,18],將樣本數(shù)據(jù)分為4組:[2,6),[6,10),[10,14),[14,18],得到頻率分布直方圖如圖所示.則下列說法不正確的是( )
3.容量為100的樣本,其數(shù)據(jù)分布在[2,18],將樣本數(shù)據(jù)分為4組:[2,6),[6,10),[10,14),[14,18],得到頻率分布直方圖如圖所示.則下列說法不正確的是( )A.樣本數(shù)據(jù)分布在[6,10)的頻率為0.32 B.樣本數(shù)據(jù)分布在[10,14)的頻數(shù)為40 C.樣本數(shù)據(jù)分布在[2,10)的頻數(shù)為40 D.估計總體數(shù)據(jù)大約有10%分布在[10,14) 組卷:211引用:10難度:0.8 -
4.下列敘述:①某人射擊1次,“射中7環(huán)”與“射中8環(huán)”是互斥事件;
②甲、乙兩人各射擊1次,“至少有1人射中目標(biāo)”與“沒有人射中目標(biāo)”是對立事件;
③拋擲一枚硬幣,連續(xù)出現(xiàn)4次正面向上,則第5次出現(xiàn)反面向上的概率大于;12
④在相同條件下,進(jìn)行大量重復(fù)試驗,可以用頻率來估計概率;則所有正確結(jié)論的序號是( )A.①②④ B.①③ C.②④ D.①② 組卷:201引用:3難度:0.6 -
 5.驚艷全世界的南非雙曲線大教堂是由倫敦著名的建筑事務(wù)所steynstudio完成的,建筑師的設(shè)計靈感源于想法:“你永無止境的愛是多么的珍貴,人們在你雄偉的翅膀下庇護(hù)”.若將如圖所示的雙曲線大教堂外形弧線的一段近似看成雙曲線y2-=1(m>0)下支的一部分,且此雙曲線的一條漸近線方程為2x-my=0,則此雙曲線的離心率為( )x2m
5.驚艷全世界的南非雙曲線大教堂是由倫敦著名的建筑事務(wù)所steynstudio完成的,建筑師的設(shè)計靈感源于想法:“你永無止境的愛是多么的珍貴,人們在你雄偉的翅膀下庇護(hù)”.若將如圖所示的雙曲線大教堂外形弧線的一段近似看成雙曲線y2-=1(m>0)下支的一部分,且此雙曲線的一條漸近線方程為2x-my=0,則此雙曲線的離心率為( )x2mA. 52B. 5C.2 D. 3組卷:79引用:5難度:0.8 -
6.在區(qū)間[0,π]上隨機(jī)取一個數(shù)θ,使得
成立的概率是( )2≤2sinθ+2cosθ≤2A. 14B. 12C. 13D.1 組卷:12引用:2難度:0.6 -
7.若圓O1:x2+y2=1與圓O2:(x-a)2+(y-2a)2=4有公共點,則實數(shù)a的取值范圍是( )
A.[- ,-355]∪[55,55]355B.[- ,355]355C.[-5,- ]∪[355,355]5D.[- ,5]5組卷:160引用:6難度:0.6
三、解答題:(本大題共6個小題,17題10分其余每道小題各12分,共70分,解答時應(yīng)寫出文字說明、證明過程或演算步驟。)
-
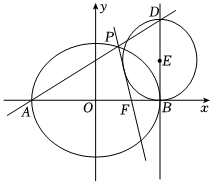 21.已知橢圓的兩個焦點與短軸的一個端點恰好圍成面積為C:x2a2+y2b2=1(a>b>0)的等邊三角形.3
21.已知橢圓的兩個焦點與短軸的一個端點恰好圍成面積為C:x2a2+y2b2=1(a>b>0)的等邊三角形.3
(1)求C的方程;
(2)如圖,設(shè)C的左,右頂點分別為A,B,右焦點為F,P是C上異于A,B的動點,直線AP與直線x=a交于點D,當(dāng)點P運動時,試判斷以BD為直徑的圓與直線PF的位置關(guān)系,并加以證明.組卷:43引用:2難度:0.6 -
22.已知橢圓C:
的左、右焦點分別為F1,F(xiàn)2,離心率為x2a2+y2b2=1(a>b>0),33為C上一點,過點F1且與y軸不垂直的直線l與C交于A,B兩點.(3,6)
(1)求C的方程;
(2)在平面內(nèi)是否存在定點Q,使得為定值?若存在,求出點Q的坐標(biāo);若不存在,請說明理由.QA?QB組卷:33引用:4難度:0.5


