2023年陜西省西安市灞橋區(qū)鐵一中濱河學(xué)校中考數(shù)學(xué)七模試卷

一、選擇題（共8小題，每小題3分）

• 1．-

  3

  5

  的倒數(shù)是（　　）

  A．- 3 5

  B． 3 5

  C．- 5 3

  D． 5 3
  組卷：540引用：40難度：0.9

  解析

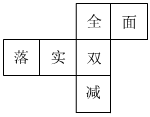• 2．一個正方體的表面展開圖如圖所示，六個面上各有一字，連起來的意思是“全面落實(shí)雙減”，把它折成正方體后，與“面”相對的字是（　　）

  A．雙

  B．減

  C．全

  D．實(shí)
  組卷：247引用：5難度：0.6

  解析

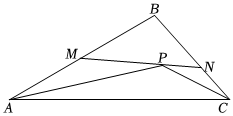• 3．如圖，點(diǎn)P為△ABC內(nèi)一點(diǎn)，過點(diǎn)P的線段MN分別交AB，BC于點(diǎn)M，N，且M，N分別在PA，PC的垂直平分線上．若∠APC=142°，則∠ABC的度數(shù)為（　　）

  A．76°

  B．104°

  C．130°

  D．140°
  組卷：1184引用：3難度：0.7

  解析

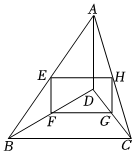• 4．如圖，D是△ABC內(nèi)一點(diǎn)，AD⊥BC，E、F、G、H分別是AB、BD、CD、AC的中點(diǎn)，添加下列哪個條件，能使得四邊形EFGH成為正方形（　　）

  A．BD=CD

  B．BD⊥CD

  C．AD=BC

  D．AB=AC
  組卷：119引用：1難度：0.5

  解析

• 5．如圖，一次函數(shù)y=kx+b（k≠0）與y=x+2的圖象相交于點(diǎn)M（m,4），則關(guān)于x,y的二元一次方程組

  kx - y = - b

  y - x = 2

  的解是（　　）

  A． x = 1 . 8 y = 4

  B． x = 2 y = 4

  C． x = 2 . 4 y = 4

  D． x = 3 y = 4
  組卷：566引用：8難度：0.7

  解析

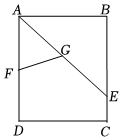• 6．如圖，在矩形ABCD中，AB=6，AD=8，AE平分∠BAD交BC于點(diǎn)E，點(diǎn)F、G分別是AD、AE的中點(diǎn)，則FG的長為（　　）

  A． 3 2

  B．5

  C．4

  D． 10
  組卷：374引用：1難度：0.5

  解析

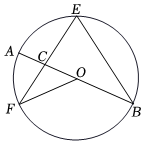• 7．如圖，AB是⊙O的直徑，EF、EB是⊙O的弦，且EF=EB，EF與AB交于點(diǎn)C，連接OF，若∠AOF=40°，則∠F的度數(shù)是（　　）

  A．35°

  B．20°

  C．40°

  D．55°
  組卷：575引用：2難度：0.5

  解析

• 8．已知點(diǎn)A（n,y₁）、B（n+2，y₂）、C（x,y₀）在二次函數(shù)y=ax²+4ax+c（a≠0）的圖象上，且C為拋物線的頂點(diǎn)，若y₀≥y₁＞y₂，則n的取值范圍是（　　）

  A．n＞-3

  B．n＜-3

  C．n＜-2

  D．n＞-2
  組卷：384引用：1難度：0.6

  解析

三、解答題（共13小題，計(jì)81分，解答應(yīng)寫出解答過程）

• 25．如圖，拋物線y=ax²-2ax-3a（a＜0）與x軸交于A、B兩點(diǎn)（點(diǎn)A在點(diǎn)B的左側(cè)），與y軸交于點(diǎn)C，頂點(diǎn)為P，拋物線的對稱軸與x軸交于點(diǎn)M，且PM=AB．
  （1）求拋物線的表達(dá)式；
  （2）矩形ADEF的邊AF在x軸負(fù)半軸上，邊AD在第二象限，AD=2，DE=3，將矩形ADEF沿x軸正方向平移得到矩形A′D′E′F′，直線A′D′與直線E′F′分別交拋物線于點(diǎn)G、H，在平移過程中，是否存在以點(diǎn)D′、F′、G、H為頂點(diǎn)的四邊形是平行四邊形？若存在，求出平移距離；若不存在，請說明理由．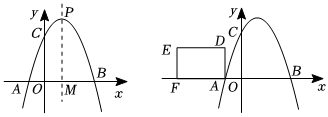
  ?
  組卷：343引用：3難度：0.2

  解析

• 26．【問題提出】
  （1）如圖1，在矩形ABCD中，AD=10，AB=12，點(diǎn)E為AD的中點(diǎn)，點(diǎn)P為矩形ABCD內(nèi)以BC為直徑的半圓上一點(diǎn)，則PE的最小值為

  ；
  【問題探究】
  （2）如圖2，在△ABC中，AD為BC邊上的高，且AD=BC=4，P為△ABC內(nèi)一點(diǎn)，當(dāng)

  S

  △

  PBC

  =

  1

  2

  S

  △

  ABC

  時，求PB+PC的最小值；
  【問題解決】
  （3）如圖3，濱河學(xué)校餐廳門口有一塊“瘋狂四季”四邊形菜園ABCD，∠ABC=∠BAD=60°，AC與BD相交于點(diǎn)P，且AD+BC=AB，過點(diǎn)A作直線BC的垂線交直線BC于點(diǎn)E，即AE⊥BE，BE=200

  3

  米，趙老師準(zhǔn)備在△ABP內(nèi)種植當(dāng)季蔬菜，邊BE的中點(diǎn)F為菜園出入口，為了種植方便，她打算在AE邊上取點(diǎn)M，并沿PM、MF修兩條人行走道，要求人行走道的總長度盡可能小，問PM+MF的長度是否存在最小值？若存在，求出其最小值；若不存在，請說明理由．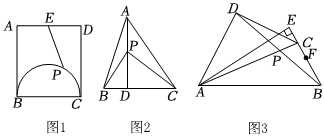
  ?
  組卷：617引用：4難度：0.3

  解析