2021-2022學年重慶八中高三（上）周考數學試卷（四）

一、單選題（本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.）

• 1．已知集合A={x|x=2ⁿ，n∈N^*}，B={x|x=2n,n∈N^*}，則（　　）

  A．A?B

  B．B?A

  C．A∩B=?

  D．A=B
  組卷：226引用：6難度：0.8

  解析

• 2．已知命題p：?x₀∈R，使得lgcosx₀＞0；命題q：?x＜0，3^x＞0，則下列命題為真命題的是（　　）

  A．p∧q

  B．p∨（￢q）

  C．（￢p）∧（￢q）

  D．p∨q
  組卷：2318引用：6難度：0.7

  解析

• 3．已知f（x）是奇函數，當x≥0時，f（x）=x²+sinπx,則f（-1）=（　　）

  A．1

  B．0

  C．-2

  D．-1
  組卷：3引用：1難度：0.8

  解析

• 4．中國的5G技術領先世界，5G技術的數學原理之一便是著名的香農公式：

  C

  =

  W

  lo

  g

  2

  （

  1

  +

  S

  N

  ）

  ．它表示：在受噪音干擾的信道中，最大信息傳遞速度C取決于信道帶寬W，信道內信號的平均功率S，信道內部的高斯噪聲功率N的大小，其中

  S

  N

  叫做信噪比．當信噪比比較大時，公式中真數里面的1可以忽略不計．按照香農公式，若帶寬W增大到原來的1.1倍，信噪比

  S

  N

  從1000提升到16000，則C大約增加了（　　）（附：lg2≈0.3）

  A．21%

  B．32%

  C．43%

  D．54%
  組卷：517引用：9難度：0.7

  解析

• 5．函數

  f

  （

  x

  ）

  =

  2

  sinx

  -

  x

  3

  |

  x

  |

  的部分圖象大致為（　　）

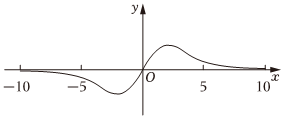
  A．	B．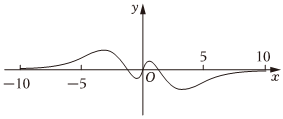
  C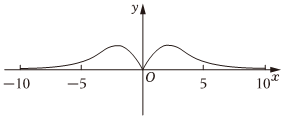．	D．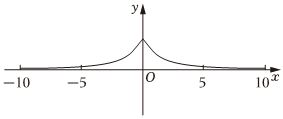
  組卷：8引用：1難度：0.8

  解析

• 6．已知

  cos

  （

  α

  -

  π

  3

  ）

  =

  1

  3

  ，則

  cos

  （

  2

  α

  +

  π

  3

  ）

  =（　　）

  A． - 8 9

  B． - 7 9

  C． 8 9

  D． 7 9
  組卷：441引用：2難度：0.7

  解析

• 7．已知函數f（x）=πx+sinπx,若 f（x²+x）≥f（m-1）恒成立，則實數m的取值范圍為（　　）

  A．.[1，+∞）

  B． （ - ∞ ， 3 4 ]

  C．.[2，+∞）

  D．.（-∞，1]
  組卷：4引用：1難度：0.7

  解析

四、解答題（本大題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟）

• 21．已知函數f（x）=（x-1）（ae^x-1）在x=1處的切線方程為y=（e-1）（x-1）．
  （1）求a的值；
  （2）若方程f（x）=b有兩個不同實根x₁、x₂，證明：

  |

  x

  1

  -

  x

  2

  |

  ＜

  eb

  e

  -

  1

  +

  1

  ．
  組卷：109引用：3難度：0.3

  解析

• 22．已知直線l₁與l₂是分別過橢圓E：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦點F₁，F₂的兩條相交但不重合的動直線，l₁與橢圓相交于點A，B．l₂與橢圓相交于點C，D，O為坐標原點，直線OA，OB，OC，OD的斜率分別為k_A，k_B，k_C，k_D，且滿足k_A+k_B=k_C+k_D．
  （1）若l₁與x軸重合，|AB|=2

  3

  ，|CD|=

  4

  3

  3

  ，試求橢圓E的方程；
  （2）在（1）的條件下，記直線l₁∩l₂=P，試問：是否存在定點M，N使得|PM|+|PN|為定值？若存在，求出定值和定點M，N的坐標；若不存在，請說明理由．
  組卷：72引用：2難度：0.6

  解析