滬教版高二(下)高考題單元試卷:第12章 圓錐曲線(08)
發布:2024/4/20 14:35:0
一、填空題(共4小題)
-
 1.如圖,橢圓的中心為原點O,長軸在x軸上,離心率,過左焦點F1作x軸的垂線交橢圓于A、A′兩點,|AA′|=4.e=22
1.如圖,橢圓的中心為原點O,長軸在x軸上,離心率,過左焦點F1作x軸的垂線交橢圓于A、A′兩點,|AA′|=4.e=22
(Ⅰ)求該橢圓的標準方程;
(Ⅱ)取平行于y軸的直線與橢圓相交于不同的兩點P、P′,過P、P′作圓心為Q的圓,使橢圓上的其余點均在圓Q外.求△PP'Q的面積S的最大值,并寫出對應的圓Q的標準方程.組卷:663引用:7難度:0.1 -
2.已知直線y=a交拋物線y=x2于A,B兩點,若該拋物線上存在點C,使得∠ACB為直角,則a的取值范圍為.
組卷:1046引用:25難度:0.5 -
3.設F為拋物線C:y2=4x的焦點,過點P(-1,0)的直線l交拋物線C于兩點A,B,點Q為線段AB的中點,若|FQ|=2,則直線l的斜率等于.
組卷:1319引用:13難度:0.5 -
4.橢圓Γ:
=1(a>b>0)的左、右焦點分別為F1,F2,焦距為2c,若直線y=x2a2+y2b2與橢圓Γ的一個交點M滿足∠MF1F2=2∠MF2F1,則該橢圓的離心率等于.3(x+c)組卷:2490引用:44難度:0.5
二、解答題(共26小題)
-
5.已知橢圓C的兩個焦點分別為F1(-1,0)、F2(1,0),短軸的兩個端點分別為B1,B2.
(1)若△F1B1B2為等邊三角形,求橢圓C的方程;
(2)若橢圓C的短軸長為2,過點F2的直線l與橢圓C相交于P,Q兩點,且,求直線l的方程.F1P⊥F1Q組卷:1387引用:43難度:0.1 -
6.設橢圓E:
的焦點在x軸上x2a2+y21-a2=1
(1)若橢圓E的焦距為1,求橢圓E的方程;
(2)設F1,F2分別是橢圓E的左、右焦點,P為橢圓E上第一象限內的點,直線F2P交y軸于點Q,并且F1P⊥F1Q,證明:當a變化時,點P在某定直線上.組卷:1434引用:12難度:0.1 -
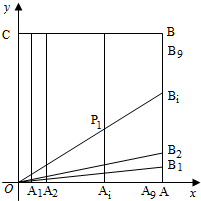 7.如圖,在正方形OABC中,O為坐標原點,點A的坐標為(10,0),點C的坐標為(0,10),分別將線段OA和AB十等分,分點分別記為A1,A2,…,A9和B1,B2,…,B9,連接OBi,過Ai作x軸的垂線與OBi,交于點Pi(i∈N*,1≤i≤9).
7.如圖,在正方形OABC中,O為坐標原點,點A的坐標為(10,0),點C的坐標為(0,10),分別將線段OA和AB十等分,分點分別記為A1,A2,…,A9和B1,B2,…,B9,連接OBi,過Ai作x軸的垂線與OBi,交于點Pi(i∈N*,1≤i≤9).
(1)求證:點Pi(i∈N*,1≤i≤9)都在同一條拋物線上,并求拋物線E的方程;
(2)過點C作直線l與拋物線E交于不同的兩點M,N,若△OCM與△OCN的面積之比為4:1,求直線l的方程.組卷:520引用:10難度:0.5 -
8.已知拋物線C:y2=4x的焦點為F.
(1)點A,P滿足.當點A在拋物線C上運動時,求動點P的軌跡方程;AP=-2FA
(2)在x軸上是否存在點Q,使得點Q關于直線y=2x的對稱點在拋物線C上?如果存在,求所有滿足條件的點Q的坐標;如果不存在,請說明理由.組卷:819引用:7難度:0.3 -
9.平面直角坐標系xOy中,已知橢圓C:
+x2a2=1(a>b>0)的離心率為y2b2,左、右焦點分別是F1,F2,以F1為圓心以3為半徑的圓與以F2為圓心以1為半徑的圓相交,且交點在橢圓C上.32
(Ⅰ)求橢圓C的方程;
(Ⅱ)設橢圓E:+x24a2=1,P為橢圓C上任意一點,過點P的直線y=kx+m交橢圓E于A,B兩點,射線PO交橢圓E于點Q.y24b2
(ⅰ)求||的值;OQOP
(ⅱ)求△ABQ面積的最大值.組卷:5512引用:17難度:0.5 -
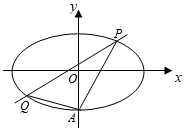 10.如圖,橢圓E:+x2a2=1(a>b>0)經過點A(0,-1),且離心率為y2b2.22
10.如圖,橢圓E:+x2a2=1(a>b>0)經過點A(0,-1),且離心率為y2b2.22
(Ⅰ)求橢圓E的方程;
(Ⅱ)經過點(1,1),且斜率為k的直線與橢圓E交于不同的兩點P,Q(均異于點A),證明:直線AP與AQ斜率之和為2.組卷:10212引用:36難度:0.5
二、解答題(共26小題)
-
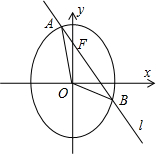 29.已知O為坐標原點,F為橢圓C:在y軸正半軸上的焦點,過F且斜率為-x2+y22=1的直線l與C交于A、B兩點,點P滿足2.OA+OB+OP=0
29.已知O為坐標原點,F為橢圓C:在y軸正半軸上的焦點,過F且斜率為-x2+y22=1的直線l與C交于A、B兩點,點P滿足2.OA+OB+OP=0
(Ⅰ)證明:點P在C上;
(Ⅱ)設點P關于點O的對稱點為Q,證明:A、P、B、Q四點在同一圓上.組卷:2607引用:11難度:0.1 -
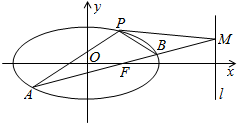 30.如圖,橢圓C:經過點P(1,x2a2+y2b2=1(a>b>0)),離心率e=32,直線l的方程為x=4.12
30.如圖,橢圓C:經過點P(1,x2a2+y2b2=1(a>b>0)),離心率e=32,直線l的方程為x=4.12
(1)求橢圓C的方程;
(2)AB是經過右焦點F的任一弦(不經過點P),設直線AB與直線l相交于點M,記PA,PB,PM的斜率分別為k1,k2,k3.問:是否存在常數λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,說明理由.組卷:4972引用:77難度:0.1


