2009-2010學年數學寒假作業（06）

一、解答題（共6小題，滿分17分）

• 1．△ABC中，三個內角A、B、C所對的邊分別為a、b、c,若B=60°，a=（

  3

  -1）c.
  （1）求角A的大小；
  （2）已知當x∈[

  π

  6

  ，

  π

  2

  ]時，函數f（x）=cos2x+asinx的最大值為3，求△ABC的面積．
  組卷：55引用：11難度：0.5

  解析

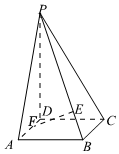• 2．如圖，已知四棱錐P-ABCD的底面ABCD是邊長為1的正方形，PD⊥底面ABCD，且PD=2．
  （1）若點E、F分別在棱PB、AD上，且

  PE

  =4

  EB

  ，

  DF

  =4

  FA

  ，求證：EF⊥平面PBC；
  （2）若點G在線段PA上，且三棱錐G-PBC的體積為

  1

  4

  ，試求線段PG的長．
  組卷：89引用：4難度：0.1

  解析

一、解答題（共6小題，滿分17分）

• 5．對于給定數列{c_n}，如果存在實常數p,q使得c_n+1=pc_n+q對于任意n∈N^*都成立，我們稱數列{c_n}是“M類數列”．
  （1）若a_n=2n,b_n=3?2ⁿ，n∈N^*，數列{a_n}、{b_n}是否為“M類數列”？若是，指出它對應的實常數p,q,若不是，請說明理由；
  （2）證明：若數列{a_n}是“M類數列”，則數列{a_n+a_n+1}也是“M類數列”；
  （3）若數列{a_n}滿足a₁=2，a_n+a_n+1=3t?2ⁿ（n∈N^*），t為常數．求數列{a_n}前2009項的和．并判斷{a_n}是否為“M類數列”，說明理由；
  （4）根據對（2）（3）問題的研究，對數列{a_n}的相鄰兩項a_n、a_n+1，提出一個條件或結論與“M類數列”概念相關的真命題，并探究其逆命題的真假．
  組卷：72引用：5難度：0.5

  解析

• 6．定義在D上的函數f（x），如果滿足：對任意x∈D，存在常數M＞0，都有|f（x）|≤M成立，則稱f（x）是D上的有界函數，其中M稱為函數f（x）的上界．已知函數

  f

  （

  x

  ）

  =

  1

  +

  a

  ?

  （

  1

  2

  ）

  x

  +

  （

  1

  4

  ）

  x

  ；

  g

  （

  x

  ）

  =

  1

  -

  m

  ?

  2

  x

  1

  +

  m

  ?

  2

  x

  ．
  （1）當a=1時，求函數f（x）在（-∞，0）上的值域，并判斷函數f（x）在（-∞，0）上是否為有界函數，請說明理由；
  （2）若函數f（x）在[0，+∞）上是以3為上界的有界函數，求實數a的取值范圍；
  （3）若m＞0，函數g（x）在[0，1]上的上界是T（m），求T（m）的取值范圍．
  組卷：393引用：25難度：0.1

  解析