2022年寧夏銀川市興慶區(qū)景博學(xué)校中考數(shù)學(xué)一模試卷

一.選擇題（共8小題，滿分24分，每小題3分）

• 1．下列圖形是軸對稱圖形而不是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：295引用：10難度：0.9

  解析

• 2．下列各式中，正確的是（　　）

  A．2a+3b=5ab

  B．m6÷m2=m3

  C． 2 + 3 = 5

  D． 18 ÷ 2 = 3
  組卷：13引用：1難度：0.8

  解析

• 3．甲、乙兩名同學(xué)本學(xué)期五次引體向上的測試成績（個數(shù)）如圖，下列判斷正確的是（　　）
  

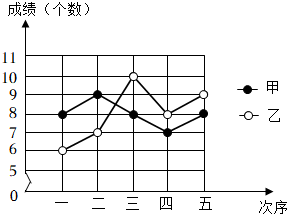
  A．甲的成績的中位數(shù)比乙的大

  B．甲的最好成績比乙的高

  C．甲的成績的平均數(shù)比乙的大

  D．甲的成績比乙穩(wěn)定
  組卷：185引用：5難度：0.7

  解析

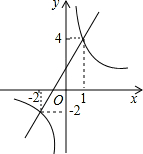• 4．一次函數(shù)y₁=kx+b（k≠0）與反比例函數(shù)y₂=

  m

  x

  （

  m

  ≠

  0

  ）

  ，在同一平面直角坐標(biāo)系中的圖象如圖所示，若y₁＜y₂，則x的取值范圍是（　　）

  A．-2＜x＜0或x＞1	B．x＞1
  C．x＜-2或0＜x＜1	D．-2＜x＜1
  組卷：1056引用：3難度：0.7

  解析

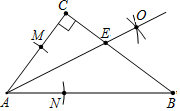• 5．如圖，在△ABC中，∠C=90°，以A為圓心，任意長為半徑畫弧，分別交AC，AB于點(diǎn)M，N，再分別以M，N為圓心，大于

  1

  2

  MN長為半徑畫弧，兩弧交于點(diǎn)O，作射線AO，交BC于點(diǎn)E．已知CE=3，BE=5，則AC的長為（　　）

  A．8

  B．7

  C．6

  D．5
  組卷：2370引用：15難度：0.6

  解析

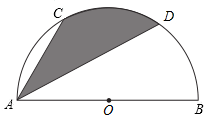• 6．如圖，已知點(diǎn)C、D是以AB為直徑的半圓的三等分點(diǎn)，弧CD的長為

  1

  3

  π

  ，則圖中陰影部分的面積為（　　）

  A． 1 6 π

  B． 3 16 π

  C． 1 24 π

  D． 1 12 π + 3 4
  組卷：1802引用：20難度：0.5

  解析

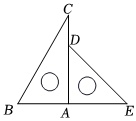• 7．一副三角板如圖放置，將三角板ADE繞點(diǎn)A逆時針旋轉(zhuǎn)α（0°＜α＜180°），使得三角板ADE的一邊所在的直線與BC垂直，則α的度數(shù)為（　　）

  A．30°、45°和60°	B．15°、60°和150°
  C．15°、30°和45°	D．45°、60°和150°
  組卷：80引用：1難度：0.6

  解析

• 8．已知正比例函數(shù)y=kx（k≠0）的函數(shù)值y隨x的增大而減小，則一次函數(shù)y=-kx+k的圖象大致是（　　）

  A．

  B．

  C．

  D．
  組卷：1343引用：27難度：0.7

  解析

三．解答題（共10小題，滿分72分）

• 25．背景閱讀：
  早在三千多年前，我國周朝數(shù)學(xué)家商高就提出：將一根直尺折成一個直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被記載與我國古代著名數(shù)學(xué)著作《周髀算經(jīng)》中，為了方便，在本題中，我們把三邊的比為3：4：5的三角形稱為（3，4，5）型三角形，例如：三邊長分別為9，12，15或

  3

  2

  ，

  4

  2

  ，

  5

  2

  的三角形就是（3，4，5）型三角形，用矩形紙片按下面的操作方法可以折出這種類型的三角形．
  實(shí)踐操作：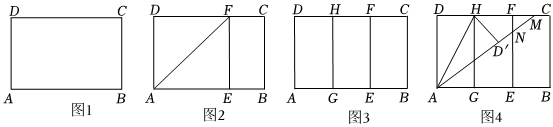
  
  如圖1，在矩形紙片ABCD中，AD=8cm,AB=12cm.
  第一步：如圖2，將圖1中的矩形紙片ABCD沿過點(diǎn)A的直線折疊，使點(diǎn)D落在AB上的點(diǎn)E處，折痕為AF，再沿EF折疊，然后把紙片展平．
  第二步：如圖3，將圖2中的矩形紙片再次折疊，使點(diǎn)D與點(diǎn)F重合，折痕為GH，然后展平，隱去AF．
  第三步：如圖4，將圖3中的矩形紙片沿AH折疊，得到△AD′H，再沿AD′折疊，折痕為AM，AM與折痕EF交于點(diǎn)N，然后展平．
  問題解決：
  （1）請?jiān)趫D4中判斷NF與ND′的數(shù)量關(guān)系，并加以證明；
  （2）請?jiān)趫D4中證明△AEN（3，4，5）型三角形；
  探索發(fā)現(xiàn)：
  （3）在不添加字母的情況下，圖4中還有哪些三角形是（3，4，5）型三角形？請找出并直接寫出它們的名稱．
  組卷：183引用：4難度：0.1

  解析

• 26．如圖，在平面直角坐標(biāo)系中，拋物線y=ax²+bx-3（a≠0）與x軸交于點(diǎn)A（-2，0）、B（4，0）兩點(diǎn)，與y軸交于點(diǎn)C．點(diǎn)P、Q分別是AB、BC上的動點(diǎn)，當(dāng)點(diǎn)P從A點(diǎn)出發(fā)，在線段AB上以每秒3個單位長度的速度向B點(diǎn)運(yùn)動，同時點(diǎn)Q從B點(diǎn)出發(fā)，在線段BC上以每秒1個單位長度的速度向C點(diǎn)運(yùn)動，其中一個點(diǎn)到達(dá)終點(diǎn)時，另一個點(diǎn)也停止運(yùn)動．設(shè)P、Q同時運(yùn)動的時間為t秒（0＜t＜2）．
  （1）求拋物線的表達(dá)式；
  （2）設(shè)△PBQ的面積為S，當(dāng)t為何值時，△PBQ的面積最大，最大面積是多少？
  （3）當(dāng)t為何值時，△PBQ是等腰三角形？
  組卷：420引用：6難度：0.3

  解析