2022-2023學(xué)年廣東省廣州大學(xué)附中八年級（上）開學(xué)數(shù)學(xué)試卷

一、單選題（30分）

• 1．

  81

  的平方根是（　　）

  A．±3

  B．3

  C．±9

  D．9
  組卷：12765引用：94難度：0.9

  解析

• 2．下面的四個圖形中，∠1與∠2是對頂角的是（　　）

  A．

  B．

  C．

  D．
  組卷：2099引用：81難度：0.9

  解析

• 3．如果點M（a+3，a+1）在直角坐標(biāo)系的x軸上，那么點M的坐標(biāo)為（　　）

  A．（0，-2）

  B．（2，0）

  C．（4，0）

  D．（0，-4）
  組卷：167引用：11難度：0.9

  解析

• 4．“x的2倍與3的和是非負(fù)數(shù)”列成不等式為（　　）

  A．2x+3≥0

  B．2x+3＞0

  C．2x+3≤0

  D．2x+3＜0
  組卷：166引用：5難度：0.7

  解析

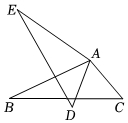• 5．如圖AC=AD，∠CAD=∠BAE，不能判斷△ABC≌△AED的是（　　）

  A．DE=CB

  B．∠C=∠D

  C．AB=AE

  D．∠B=∠E
  組卷：388引用：2難度：0.6

  解析

• 6．方程組

  2 x + ky = 4

  x - 2 y = 0

  的解為正數(shù)，則k的取值范圍是（　　）

  A．k＞4

  B．k≥4

  C．k＞0

  D．k＞-4
  組卷：81引用：5難度：0.9

  解析

• 7．一個正多邊形每個內(nèi)角與它相鄰?fù)饨堑亩葦?shù)比為3：1，則這個正多邊形是（　　）

  A．正方形

  B．正六邊形

  C．正八邊形

  D．正十邊形
  組卷：1902引用：23難度：0.7

  解析

三、解答題（72分）

• 22．在△ABC中，AB=2，BC=4，CD⊥AB于D．
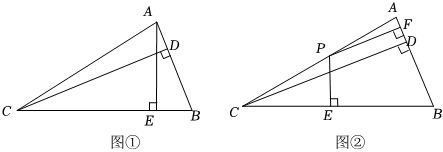
  （1）如圖①，已知AE⊥BC于E，求證：CD=2AE；
  （2）如圖②，P是線段AC上任意一點（P不與A、C重合），過P作PE⊥BC于E，PF⊥AB于F，求證：2PE+PF=CD；
  （3）在圖②中，若P是AC延長線上任意一點，其他條件不變，請畫出圖形并直接寫出PE、PF、CD之間的關(guān)系．
  組卷：211引用：1難度：0.1

  解析

• 23．如圖1，已知線段AB、CD相交于點O，連接AC、BD，則我們把形如這樣的圖形稱為“8字型”．
  （1）求證：∠A+∠C=∠B+∠D；
  （2）如圖2，若∠CAB和∠BDC的平分線AP和DP相交于點P，且與CD、AB分別相交于點M、N．
  ①以線段AC為邊的“8字型”有

  個，以點O為交點的“8字型”有

  個；
  ②若∠B=100°，∠C=120°，求∠P的度數(shù)；
  ③若角平分線中角的關(guān)系改為“∠CAP=

  1

  3

  ∠CAB，∠CDP=

  1

  3

  ∠CDB”，試探究∠P與∠B、∠C之間存在的數(shù)量關(guān)系，并證明理由．
  
  組卷：3193引用：17難度：0.6

  解析