2023年河南省南陽市內(nèi)鄉(xiāng)縣中考數(shù)學(xué)一模試卷
發(fā)布:2024/4/20 14:35:0
一、選擇題(每小題3分,共30分)
-
1.在實際生活中,我們經(jīng)常用正數(shù)和負(fù)數(shù)來表示意義相反的兩個量,-2023的相反數(shù)是( )
A.2023 B.-2023 C.- 12023D. 12023組卷:37引用:2難度:0.9 -
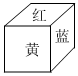 2.如圖,某正方體三組相對的兩個面的顏色相同,分別為紅,黃,藍(lán)三色,其展開圖不可能是( )
2.如圖,某正方體三組相對的兩個面的顏色相同,分別為紅,黃,藍(lán)三色,其展開圖不可能是( )A. 
B. 
C. 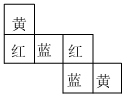
D.  組卷:143引用:4難度:0.8
組卷:143引用:4難度:0.8 -
 3.下面是投影屏上出示的搶答題,需要回答括號內(nèi)符號代表的內(nèi)容:
3.下面是投影屏上出示的搶答題,需要回答括號內(nèi)符號代表的內(nèi)容:
如圖:已知直線b∥c,a⊥b,求證:a⊥c.
證明:∵a⊥b(已知),
∴∠1=(☆)(垂直的定義)
又∵b∥c(已知),
∴∠1=∠2(◎),
∴∠2=∠1=90°(@)
∴a⊥c(※).
則下列回答錯誤的是( )A.☆代表90° B.◎代表同位角相等,兩直線平行 C.@代表等量代換 D.※代表垂直的定義 組卷:138引用:4難度:0.7 -
4.下列計算正確的是( )
A. 12-3=3B.(-a2)3=a6 C.(a-b)2=a2-b2(b≠0) D.3xy-2yx=xy 組卷:114引用:4難度:0.7 -
 5.如圖所示,點O是矩形ABCD的對角線AC的中點,點E為AD的中點.若AB=4,BC=6,則△BOE的周長為( )
5.如圖所示,點O是矩形ABCD的對角線AC的中點,點E為AD的中點.若AB=4,BC=6,則△BOE的周長為( )A.10 B.8+ 13C.7+ 13D.8 組卷:209引用:5難度:0.6 -
6.已知當(dāng)x<0時,反比例函數(shù)
的函數(shù)值隨自變量的增大而減小,則關(guān)于x的一元二次方程x2-2x+1-k=0根的情況是( )y=kxA.有兩個相等的實數(shù)根 B.沒有實數(shù)根 C.有兩個不相等的實數(shù)根 D.跟k的取值有關(guān) 組卷:119引用:3難度:0.7 -
 7.某地區(qū)經(jīng)過三年的鄉(xiāng)村振興建設(shè),農(nóng)村的經(jīng)濟收入是振興前的2倍.為更好地了解該地區(qū)農(nóng)村的經(jīng)濟收入變化情況,統(tǒng)計了該地區(qū)鄉(xiāng)村振興建設(shè)前后農(nóng)村的經(jīng)濟收入構(gòu)成比例,繪制了下面的扇形統(tǒng)計圖,則下列說法錯誤的是( )
7.某地區(qū)經(jīng)過三年的鄉(xiāng)村振興建設(shè),農(nóng)村的經(jīng)濟收入是振興前的2倍.為更好地了解該地區(qū)農(nóng)村的經(jīng)濟收入變化情況,統(tǒng)計了該地區(qū)鄉(xiāng)村振興建設(shè)前后農(nóng)村的經(jīng)濟收入構(gòu)成比例,繪制了下面的扇形統(tǒng)計圖,則下列說法錯誤的是( )A.鄉(xiāng)村振興建設(shè)后,養(yǎng)殖收入是振興前的2倍 B.鄉(xiāng)村振興建設(shè)后,種植收入減少 C.鄉(xiāng)村振興建設(shè)后,其它收入是振興前的2.5倍 D.鄉(xiāng)村振興建設(shè)后,養(yǎng)殖收入與第三產(chǎn)業(yè)收入的總和超過了經(jīng)濟收入的一半 組卷:72引用:2難度:0.6
三、解答題(共8小題,共75分)
-
22.(1)【教材呈現(xiàn)】
圓周角定理推論:90°的圓周角所對的弦是直徑.
如圖①,已知:A、B、C三點在⊙O上,∠ACB=90°.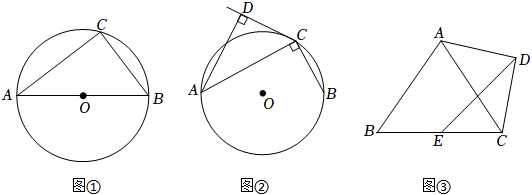
求證:AB為⊙O直徑.
證明:∵AB為圓周角∠ACB所對的弦,∠AOB為圓周角∠ACB所對應(yīng)的圓心角,
∴∠ACB=∠AOB,且∠ACB=90°.12
∴∠AOB=180°…( )
∴點O在線段AB上,即三點共線.則AB為⊙O的直徑.
上述推理:得∠AOB=180°,依據(jù)為 .
(2)【小試牛刀】
如圖②,A、B、C三點在⊙O上且∠ACB=90°,過點A作AD垂直⊙O的切線CD于點D,若AC=4,BC=3.求AD的長.
(3)【拓展應(yīng)用】
如圖③,已知△ABC是等邊三角形,以AC為底邊在△ABC外作等腰直角△ACD,點E為BC的中點,連結(jié)DE,請直接寫出∠ADE+∠DEC的度數(shù).組卷:352引用:2難度:0.3 -
 23.問題情境:數(shù)學(xué)活動課上,老師組織同學(xué)們以“正方形”為主題開展數(shù)學(xué)活動.
23.問題情境:數(shù)學(xué)活動課上,老師組織同學(xué)們以“正方形”為主題開展數(shù)學(xué)活動.
動手實踐:
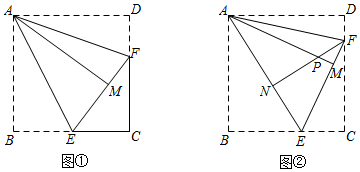
(1)如圖①,已知正方形紙片ABCD,勤奮小組將正方形紙片沿過點A的直線折疊,使點B落在正方形ABCD的內(nèi)部,點B的對應(yīng)點為點M,折痕為AE,再將紙片沿過點A的直線折疊,使AD與AM重合,折痕為AF,易知點E、M、F共線,則∠EAF=度.
拓展應(yīng)用:
(2)如圖②,騰飛小組在圖①的基礎(chǔ)上進(jìn)行如下操作:將正方形紙片沿EF繼續(xù)折疊,使得點C的對應(yīng)點為點N,他們發(fā)現(xiàn),當(dāng)點E的位置不同時,點N的位置也不同,當(dāng)點E在BC邊的某一位置時,點N恰好落在折痕AE上.
①則∠CFE=度.
②設(shè)AM與NF的交點為點P,運用(1)、(2)操作所得結(jié)論,求證:△ANP≌△FNE.
解決問題:
(3)在圖②中,若AB=3,請直接寫出線段MP的長.組卷:1094引用:9難度:0.3


