2022-2023學年江西省南昌市鐵路一中高一(下)月考數學試卷(3月份)
發布:2024/7/22 8:0:9
一、單選題(本大題共8小題,共40.0分.在每小題列出的選項中,選出符合題目的一項)
-
1.已知角α=8,則角α的終邊在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限 組卷:335引用:2難度:0.8 -
2.與-1050°終邊相同的最小正角是( )
A.-30° B.60° C.30° D.-60° 組卷:204引用:2難度:0.8 -
3.已知sin(
)=π4+α,則cos(23)的值等于( )π4-αA. -23B. 23C. 53D. ±53組卷:4725引用:8難度:0.9 -
4.sin1°,sin1,sinπ°的大小順序是( )
A.sin1°<sin1<sinπ° B.sin1°<sinπ°<sin1 C.sinπ°<sin1°<sin1 D.sin1<sin1°<sinπ° 組卷:75引用:3難度:0.9 -
5.已知角α的終邊上有一點P(1,3),則
的值為( )cos(3π2-α)+2cos(-π+α)A. 1010B. 102C. -1010D. -102組卷:575引用:5難度:0.7 -
6.已知函數f(x)是定義在R上的奇函數,f(-x)=f(x+2),則f(2020)=( )
A.-1 B.0 C.1 D.2 組卷:225引用:2難度:0.7 -
7.函數y=2|x|sin2x的圖象可能是( )
A. 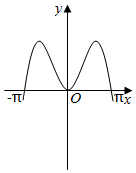
B. 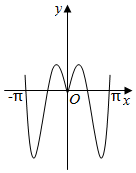
C. 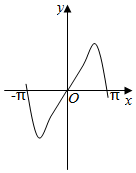
D. 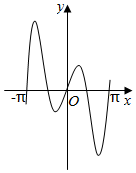 組卷:8049引用:113難度:0.7
組卷:8049引用:113難度:0.7
四、解答題(本大題共6小題,共70.0分.解答應寫出文字說明,證明過程或演算步驟)
-
21.人臉識別技術應用在各行各業,改變著人類的生活,所謂人臉識別,就是利用計算機分析人臉視頻或者圖像,并從中提取出有效的識別信息,最終判別人臉對象的身份.在人臉識別中為了檢測樣本之間的相似度主要應用距離的測試,常用的測量距離的方式有曼哈頓距離和余弦距離.假設二維空間兩個點A(x1,y1),B(x2,y2),曼哈頓距離d(A,B)=|x1-x2|+|y1-y2|.
余弦相似度:cos(A,B)=.x1x21+y21×x2x22+y22+y1x21+y21×y2x22+y22
余弦距離:1-cos(A,B).
(1)若,A(1,-3),求A,B之間的d(A,B)和余弦距離;B(12,32)
(2)已知M(sinα,cosα),N(sinβ,cosβ),Q(sinβ,-cosβ),若cos(M,N)=,cos(M,Q)=13,求tanαtanβ的值.12組卷:85引用:7難度:0.7 -
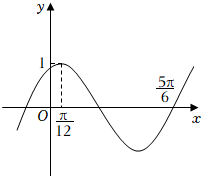 22.函數的部分圖象如圖所示.f(x)=cos(ωx+φ)(ω>0,|φ|<π2)
22.函數的部分圖象如圖所示.f(x)=cos(ωx+φ)(ω>0,|φ|<π2)
(1)求f(x)的解析式;
(2)若,[f(x)]2-mf(x)-1≤0,求實數m的取值范圍;?x∈[-π4,π4]
(3)求實數a和正整數n,使得函數F(x)=f(x)-a在[0,nπ]上恰有2021個零點.組卷:499引用:4難度:0.3


