2022-2023學年廣東省廣州市白云區培英中學高三（上）期末數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知復數z在復平面上對應的點為（-1，1），則（　　）

  A．z+1是實數	B．z+1是純虛數
  C．z+i是實數	D．z+i是純虛數
  組卷：162引用：6難度：0.8

  解析

• 2．已知集合

  A

  =

  {

  x

  |

  y

  =

  4

  x

  -

  x

  2

  }

  ，B={x|1-x＞0}，則A∪B=（　　）

  A．{x|0≤x＜1}

  B．{x|x≤4}

  C．{x|1＜x≤4}

  D．{x|x≥0}
  組卷：162引用：6難度：0.9

  解析

• 3．已知等比數列{a_n}的各項都是正數，且

  3

  a

  1

  ，

  1

  2

  a

  3

  ，

  2

  a

  2

  成等差數列，則

  a

  8

  +

  a

  7

  a

  5

  +

  a

  4

  =（　　）

  A．8

  B．16

  C．27

  D．4
  組卷：131引用：1難度：0.6

  解析

• 4．函數f（x）=

  x

  ?

  2

  x

  1

  -

  x

  2

  的部分圖象大致為（　　）

  A．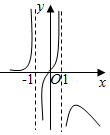

  B．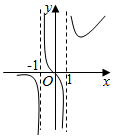

  C．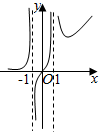

  D．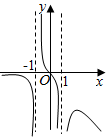
  組卷：311引用：5難度：0.7

  解析

• 5．對于R上可導的任意函數f（x），若滿足（1-x）f'（x）≥0，則必有（　　）

  A．f（0）+f（2）＜2f（1）	B．f（0）+f（2）≤2f（1）
  C．f（0）+f（2）＞2f（1）	D．f（0）+f（2）≥2f（1）
  組卷：79引用：2難度：0.6

  解析

• 6．已知圓O的半徑為R，若A，B是其圓周上的兩個三等分點，則

  OA

  ?

  AB

  的值等于（　　）

  A． 3 2 R 2

  B． - 1 2 R 2

  C． - 3 2 R 2

  D． - 3 2 R 2
  組卷：32引用：6難度：0.9

  解析

• 7．函數

  f

  （

  x

  ）

  =

  A

  sin

  （

  ωx

  +

  φ

  ）

  （

  A

  ＞

  0

  ，

  ω

  ＞

  0

  ，

  |

  φ

  |

  ＜

  π

  2

  ）

  的圖象與y軸交于點M（0，-1），圖象上離y軸最近的最高點為

  N

  （

  π

  4

  ，

  2

  ）

  ，若對?x₁，x₂∈（-a,a），x₁≠x₂，恒有f（x₁）≠f（x₂），則實數a的最大值為（　　）

  A． π 4

  B． π 6

  C． π 8

  D． π 12
  組卷：171引用：2難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．在平面直角坐標系xOy中，已知圓A：（x+2）²+y²=8，B（2，0），動圓P經過點B且與圓A相外切，記動圓的圓心P的軌跡為C．
  （1）求C的方程；
  （2）試問，在x軸上是否存在點M，使得過點M的動直線l交C于E，F兩點時，恒有∠EAM=∠FAM？若存在，求出點M的坐標；若不存在，請說明理由．
  組卷：145引用：3難度：0.6

  解析

• 22．已知函數f（x）=[x²-（a+1）x+1]?e^x，a∈R．
  （Ⅰ）討論函數f（x）的單調性；
  （Ⅱ）若a=-1，對任意x₁，x₂∈（0，∞），當x₁＞x₂時，不等式|f（x₁）-f（x₂）|＜m

  （

  e

  2

  x

  1

  -

  e

  2

  x

  2

  ）

  恒成立，求實數m的取值范圍．
  組卷：248引用：6難度：0.2

  解析