2022-2023學年重慶203中學高三（上）第二次質檢數學試卷

一、選擇題：本題共8個小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x||x-2|≤2}，B={-3，-2，1，2}，則A∩B=（　　）

  A．{-2，1}

  B．{-2，2}

  C．{-3，2}

  D．{1，2}
  組卷：74引用：3難度：0.9

  解析

• 2．根據分類變量x與y的觀察數據，計算得到K²=3.174，依據下表給出的K²獨立性檢驗中（　　）
  

  P（K2≥k）	0.1	0.05	0.01	0.005	0.001
  k	2.706	3.841	6.635	7.879	10.828

  A．有95%的把握認為變量x與y獨立

  B．有95%的把握認為變量x與y不獨立

  C．變量x與y獨立，這個結論犯錯誤的概率不超過10%

  D．變量x與y不獨立，這個結論犯錯誤的概率不超過10%
  組卷：129引用：2難度：0.8

  解析

• 3．函數

  f

  （

  x

  ）

  =

  sin

  （

  πx

  ）

  e

  x

  +

  e

  -

  x

  的圖象大致是（　　）

  A．

  B．

  C．

  D．
  組卷：167引用：12難度：0.9

  解析

• 4．經研究發現，某昆蟲釋放信息素ts后，在距釋放處xm的地方測得信息素濃度y滿足lny=-

  1

  2

  lnt-

  K

  t

  x²+A，其中A，K為非零常數．已知釋放1s后，在距釋放處2m的地方測得信息素濃度為a,則釋放信息素4s后，信息素濃度為

  a

  2

  的位置距釋放處的距離為（　　）

  A． 1 4 m

  B． 1 2 m

  C．2m

  D．4m
  組卷：105引用：10難度：0.7

  解析

• 5．六名大四學生（其中4名男生、2名女生）被安排到A、B、C三所學校實習，每所學校2人，且2名女生不到同一學校，也不到C學校，男生甲不到A學校，則不同的安排方法共有（　　）

  A．9種

  B．12種

  C．15種

  D．18種
  組卷：234引用：6難度：0.7

  解析

• 6．曲線y=2lnx上的點到直線x-y+2ln2=0的最短距離是（　　）

  A．2

  B．2-ln2

  C．ln 2

  D． 2
  組卷：184引用：7難度：0.6

  解析

• 7．若α，β∈（0，

  π

  2

  ），且（1+cos2α）（1+sinβ）=sin2αcosβ，則下列結論正確的是（　　）

  A． α + β = π 2

  B． α + β 2 = π 2

  C． 2 α - β = π 2

  D． α - β = π 2
  組卷：854引用：5難度：0.5

  解析

四、解答題：本大題共6小題，共70分．請在答題卡指定區域內作答，解答時應寫出必要的文字說明，證明過程或演算步驟．

• 21．2022年冬季奧林匹克運動會主辦城市是北京，北京成為第一個舉辦過夏季奧林匹克運動會和冬季奧林匹克運動會以及亞洲運動會三項國際賽事的城市．為迎接冬奧會的到來，某地很多中小學開展了模擬冬奧會賽事的活動，為了深入了解學生在“自由式滑雪”和“單板滑雪”兩項活動的參與情況，在該地隨機選取了10所學校進行研究，得到如下數據：
  
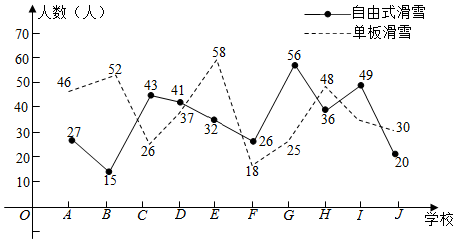
  （1）在這10所學校中隨機選取3所來調查研究，求在抽到學校至少有一個參與“自由式滑雪”超過40人的條件下，“單板滑雪”不超過30人的概率；
  （2）現在有一個“單板滑雪”集訓營，對“滑行、轉彎、停止”這3個動作技巧進行集訓，且在集訓中進行了多輪測試．規定：在一輪測試中，這3個動作中至少有2個動作達到“優秀”．則該輪測試記為“優秀”，在集訓測試中，小明同學3個動作中每個動作達到“優秀”的概率均為

  1

  3

  ，每個動作互不影響且每輪測試互不影響．如果小明同學在集訓測試中要想獲得“優秀”的次數的平均值達到3次，那么理論上至少要進行多少輪測試？
  組卷：161引用：3難度：0.6

  解析

• 22．設f（x）=ae^x-2x-1，其中a∈R．
  （1）討論f（x）的單調性；
  （2）令F（x）=e^xf（x）+

  5

  4

  a

  （a≠0），若F（x）≤0在R上恒成立，求a的最小值．
  組卷：133引用：8難度：0.3

  解析