2023-2024學年北京四中高三（上）開學數學試卷

一、選擇題（本大題共10小題，每小題4分，共40分）

• 1．集合A={x|-1≤x≤2}，B={x|x＜1}，則A∩（?_RB）=（　　）

  A．{x|x＞1}

  B．{x|x≥1}

  C．{x|1＜x≤2}

  D．{x|1≤x≤2}
  組卷：263引用：33難度：0.9

  解析

• 2．在

  （

  x

  -

  2

  ）

  6

  的展開式中，x³的系數為（　　）

  A． - 40 2

  B． 40 2

  C．-40

  D．40
  組卷：657引用：4難度：0.9

  解析

• 3．已知a=4^0.1，b=2^0.6，c=log₄0.6，則a,b,c的大小關系為（　　）

  A．c＜a＜b

  B．c＜b＜a

  C．a＜b＜c

  D．b＜a＜c
  組卷：559引用：8難度：0.8

  解析

• 4．有10名學生，其中4名男生，6名女生，從中任選2名學生，其中恰好有1名男生的概率是（　　）

  A． 8 15

  B． 6 25

  C． 2 15

  D． 4 45
  組卷：109引用：2難度：0.7

  解析

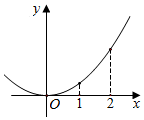• 5．已知函數f（x）在R上可導，其部分圖象如圖所示，設

  f

  （

  2

  ）

  -

  f

  （

  1

  ）

  2

  -

  1

  =a,則下列不等式正確的是（　　）

  A．f′（1）＜f′（2）＜a	B．f′（1）＜a＜f′（2）
  C．f′（2）＜f′（1）＜a	D．a＜f′（1）＜f′（2）
  組卷：1057引用：16難度：0.9

  解析

• 6．給出下面四個命題：
  ①“直線a,b不相交”是“直線a,b為異面直線”的充分而不必要條件；
  ②“l⊥平面α”是“直線l⊥平面α內所有直線”的充要條件；
  ③“a平行于b所在的平面”是“直線a∥直線b”的充要條件；
  ④“直線a平行于α內的一條直線”是“直線a∥平面α”的必要而不充分條件．
  其中正確命題的序號是（　　）

  A．①③

  B．②③

  C．②④

  D．③④
  組卷：31引用：1難度：0.7

  解析

• 7．“蘇州碼子”發源于蘇州，在明清至民國時期，作為一種民間的數字符號曾經流行一時，廣泛應用于各種商業場合.110多年前，詹天佑主持修建京張鐵路，首次將“蘇州碼子”刻于里程碑上．“蘇州碼子”計數方式如下：〡（1）、〢（2）、〣（3）、〤（4）、〥（5）、〦（6）、〧（7）、〨（8）、〩（9）、〇（0）．為了防止混淆，有時要將“〡”“〢”“〣”橫過來寫．已知某鐵路的里程碑所刻數字代表距離始發車站的里程，每隔2公里擺放一個里程碑，若在A點處里程碑上刻著“〣〤”，在B點處里程碑刻著“〩〢”，則從A點到B點里程碑的個數應為（　　）

  A．29

  B．30

  C．58

  D．59
  組卷：113引用：5難度：0.8

  解析

三、解答題（共6小題，共85分）

• 20．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1的右焦點為（1，0），且經過點A（0，1）．
  （Ⅰ）求橢圓C的方程；
  （Ⅱ）設O為原點，直線l：y=kx+t（t≠±1）與橢圓C交于兩個不同點P、Q，直線AP與x軸交于點M，直線AQ與x軸交于點N．若|OM|?|ON|=2，求證：直線l經過定點．
  組卷：7226引用：18難度：0.5

  解析

• 21．正實數構成的集合A={a₁，a₂，?，a_n}（n≥2），定義A?A={a_i?a_j|a_i，a_j∈A，且i≠j}．當集合A?A中的元素恰有

  n

  （

  n

  -

  1

  ）

  2

  個數時，稱集合A具有性質Ω．
  （Ⅰ）判斷集合A₁={1，2，4}，A₂={1，2，4，8}是否具有性質Ω；
  （Ⅱ）若集合A具有性質Ω，且A中所有元素能構成等比數列，A?A中所有元素也能構成等比數列，求集合A中的元素個數的最大值；
  （Ⅲ）若集合A具有性質Ω，且A?A中的所有元素能構成等比數列．問：集合A中的元素個數是否存在最大值？若存在，求出該最大值；若不存在，請說明理由．
  組卷：65引用：3難度：0.2

  解析