2021-2022學年江西省宜春市高二（下）期末數學試卷（理科）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．復數z滿足

  z

  （

  1

  +

  i

  ）

  =

  |

  1

  2

  -

  3

  2

  i

  |

  （i為虛數單位），則在復平面內復數z對應的點在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：31引用：1難度：0.8

  解析

• 2．若a,b,c∈R，則下列命題正確的是（　　）

  A．若a＞b,則a3＞b3	B．若a＞b,則ac2＞bc2
  C．若a＞b,則 1 a ＜ 1 b	D．若a＞b,c＞d,則ac＞bd
  組卷：62引用：3難度：0.7

  解析

• 3．根據分類變量..與y的觀察數據計算得：K²=5.974．根據下表給出的K²獨立性檢驗中的小概率值和相應的臨界值，作出下列判斷，正確的是（　　）
  

  P（K2≥k0）	0.100	0.050	0.025	0.010	0.001
  k0	2.706	3.841	5.024	6.635	10.828

  A．有99%的把握認為變量x與y獨立

  B．有99%的把握認為變量x與y不獨立

  C．變量x與y不獨立，這個結論犯錯誤的概率不超過2.5%

  D．變量x與y獨立，這個結論犯錯誤的概率不超過2.5%
  組卷：25引用：1難度：0.8

  解析

• 4．在同一坐標系中，將曲線x²+y²=1變為曲線

  x

  ′

  2

  4

  +

  y

  ′

  2

  9

  =

  1

  的一個伸縮變換是（　　）

  A． x ′ = 2 x y ′ = 3 y	B． x ′ = 1 2 x y ′ = 1 3 y
  C． x = 1 2 x ′ y = 3 y ′	D． x = 2 x ′ y = 1 3 y ′
  組卷：11引用：1難度：0.7

  解析

• 5．將一枚均勻的骰子連續投擲兩次，記兩次向上的點數之和為隨機變量ξ，則P（ξ＞4）=（　　）

  A． 1 6

  B． 5 6

  C． 8 11

  D． 11 12
  組卷：11引用：1難度：0.8

  解析

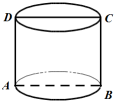• 6．如圖所示圓柱的軸截面ABCD的周長為定值，則（　　）

  A．圓柱的體積有最小值，此時高與底面圓的直徑之比為1

  B．圓柱的體積有最小值，此時高與底面圓的半徑之比為1

  C．圓柱的體積有最大值，此時高與底面圓的直徑之比為1

  D．圓柱的體積有最大值，此時高與底面圓的半徑之比為1
  組卷：24引用：1難度：0.6

  解析

• 7．隨機變量ξ的分布列如表：
  

  ξ	0	4x	2 1 - x 2
  P	1 4	k	1 2

  則當E（ξ）取最大值時，D（ξ）=（　　）

  A． 2 3

  B． 5 9

  C．1

  D． 4 3
  組卷：224引用：1難度：0.5

  解析

三、解答題：共70分．解答應寫出文字說明、證明過程或演算步驟．

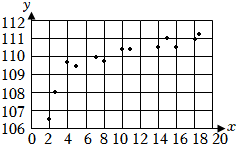• 21．2022年2月4日至2月20日第24屆冬奧會在北京舉行，本屆冬奧會吉祥物“冰墩墩”自亮相以來就好評不斷，一個原因是主辦方的廣泛宣傳．某課外學習小組通過收集整理出了宣傳力度（x）與好評量（y）之間的散點圖（如圖所示），根據散點圖中的數據，令

  s

  =

  x

  ，

  t

  =

  1

  x

  統計整理得到（s_i，y_i）與（t_i，y_i）（i=1，2，3，…，13）的如下數據表（如圖所示），現計劃用

  y

  =

  a

  +

  b

  x

  或

  y

  =

  c

  +

  d

  x

  建立y關于x的回歸方程．
  

  x		y		s		t
  10.15		109.94		3.04		0.16
  n ∑ i = 1 s i y i - 13 s ? y	13 ∑ i = 1 t i y i - 13 t ? y		13 ∑ i = 1 s 2 i - 13 x 2		13 ∑ i = 1 t 2 i - 13 t 2		13 ∑ i = 1 y 2 i - 13 y 2
  13.94	-2.1		11.67		0.21		21.22

  （1）設（s_i，y_i）與（t_i，y_i）（i=1，2，3，…，13）的相關系數分別為r₁，r₂，求r₁，r₂的值并根據其意義判斷哪種模型更合適建立y與x的回歸方程，請求出該方程；
  附：參考數據和公式：

  4

  .

  4562

  =

  2

  .

  1109

  ，

  247

  .

  6374

  =

  15

  .

  7365

  ，回歸直線方程v=α+βu的斜率和截距的最小二乘法估計分別為：

  ?

  β

  =

  n

  ∑

  i

  =

  1

  u

  i

  v

  i

  -

  n

  u

  ?

  v

  n

  ∑

  i

  =

  1

  u

  2

  i

  -

  n

  u

  2

  ，

  ?

  α

  =

  v

  -

  ?

  β

  u

  ，相關系數計算公式：

  r

  =

  n

  ∑

  i

  =

  1

  u

  i

  v

  i

  -

  n

  u

  ?

  v

  n

  ∑

  i

  =

  1

  u

  2

  i

  -

  n

  u

  2

  ?

  n

  ∑

  i

  =

  1

  v

  2

  i

  -

  n

  v

  2

  ．
  （2）為發揮線上購物的優越性，現主辦方在某網購平臺推出一款以“冰墩墩”為原型的紀念品進行售賣，網購平臺為提高銷售量，組織A，B，C三家網店開展“秒殺”搶購活動．其中甲在A家搶購一個訂單，乙在B家搶購一個訂單，丙在C家搶購一個訂單，若三人在三家網店訂單“秒殺”成功的概率均為p,且三人是否搶購成功互不影響，記三人搶購到的訂單總數為隨機變量Z．
  （ⅰ）求Z的分布列及E（Z）；
  （ⅱ）若每個訂單由k（k≥2，k∈N^*）個“冰墩墩”構成，記三人搶購到的“冰墩墩”總數量為T，假設

  p

  =

  1

  k

  -

  k

  -

  1

  2

  k

  ，求E（T）取最小值時正整數k的值．
  組卷：322引用：1難度：0.3

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  cos

  （

  -

  x

  ）

  e

  x

  （e為自然對數的底數）．
  （1）求函數f（x）的單調遞增區間；
  （2）若不等式

  af

  （

  x

  ）

  -

  1

  e

  ＞

  0

  在

  x

  ∈

  （

  0

  ，

  1

  2

  ]

  上恒成立，求實數a的取值范圍；
  （3）證明：

  f

  （

  1

  ）

  +

  f

  （

  1

  2

  ）

  +

  ?

  +

  f

  （

  1

  n

  ）

  ＞

  n

  -

  1

  e

  （

  n

  ∈

  N

  *

  ）

  ．
  組卷：31引用：1難度：0.6

  解析