2023-2024學年廣東省深圳市福田區、鹽田區十校聯考七年級(上)期中數學試卷
發布:2024/10/3 14:0:2
一.選擇題:(每小題只有一個正確選項,每小題3分,共計30分)
-
1.若向前走5步表示為+5步,則向后3步應表示為( )
A.-3步 B.+3步 C.-8步 D.+2步 組卷:42引用:1難度:0.9 -
2.用一個平面截下列幾何體,無論怎樣截,截面形狀都不發生改變的是( )
A. 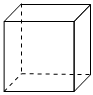
正方體B. 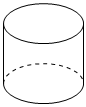
圓柱C. 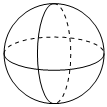
球D. 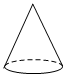
圓錐組卷:772引用:10難度:0.7 -
3.圖中屬于柱體的個數是( )

A.3 B.4 C.5 D.6 組卷:1878引用:19難度:0.9 -
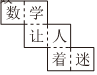 4.如圖,將圖中的紙片折起來可以做成一個正方體,這個正方體“讓”字所在面的對面是( )字.
4.如圖,將圖中的紙片折起來可以做成一個正方體,這個正方體“讓”字所在面的對面是( )字.A.數 B.學 C.著 D.迷 組卷:236引用:5難度:0.6 -
5.下列數中:-12,(-1)2,-(-1),-|-1|,負數的個數是( )
A.4個 B.3個 C.2個 D.1個 組卷:146引用:2難度:0.8 -
6.檢查四個籃球的質量,把超過標準的克數記為正數,不足標準質量的克數記為負數,結果如下表:
其中質量最好的是( )籃球編號 甲 乙 丙 丁 與標準質量的差(g) +4 +7 -3 -8 A.甲 B.乙 C.丙 D.丁 組卷:471引用:6難度:0.8 -
7.下列變形中,正確的是( )
A.3a3-a2=2a B.3a2-a2=2a2 C.3a2+2d2=5a4 D.-3a2+2a2=-5a2 組卷:65引用:1難度:0.8
三.解答題(7小題,共55分)
-
 21.學校體育節要舉辦足球賽,若有5支球隊進行單循環比賽(即全部比賽過程中任何一隊都要分別與其他各隊比賽一場且只比賽一場),則該校一共要安排多少場比賽?
21.學校體育節要舉辦足球賽,若有5支球隊進行單循環比賽(即全部比賽過程中任何一隊都要分別與其他各隊比賽一場且只比賽一場),則該校一共要安排多少場比賽?
構建模型:
生活中的許多實際問題,往往需要構建相應的數學模型,利用模型的思想來解決問題.為解決上述問題,我們構建如下數學模型:
(1)如圖①,我們可以在平面內畫出5個點(任意3個點都不在同一條直線上),其中每個點各代表一支足球隊,兩支球隊之間比賽一場就用一條線段把它們連接起來.由于每支球隊都要與其他各隊比賽一場,即每個點與另外4個點都可連成一條線段,這樣一共連成5×4條線段,而每兩個點之間的線段都重復計算了一次,實際只有=10條線段,所以該校一共要安排10場比賽.5×42
(2)若學校有6支足球隊進行單循環比賽,借助圖②,可知一共要安排 場比賽.
(3)根據以上規律,若學校有n支足球隊進行單循環比賽,則一共要安排 場比賽.
實際應用:
(4)老師為了讓數學興趣班的同學互相認識,請班上35位同學每兩個人都相互握一次手,全班同學總共握手 次.
拓展提高:
(5)往返于深圳和潮汕的同一輛高速列車,中途經惠州、陸豐、普寧、潮陽4個車站(每種車票票面都印有上車站名稱與下車站名稱),那么在這段線路上往返行車,要準備多少種車票?請你求出來.組卷:295引用:3難度:0.7 -
22.如圖,已知數軸上點A表示的數為6,B是數軸上在A左側的一點,且A,B兩點間的距離為10.動點P從點A出發,以每秒1個單位長度的速度沿數軸向左勻速運動,設運動時間為t(t>0)秒.
(1)數軸上點B表示的數是 ,點P表示的數是 (用含t的代數式表示);
(2)動點Q從點B與點P同時出發,以每秒4個單位長度的速度沿數軸向右勻速運動,求:出發幾秒后,點P與點Q相遇?
(3)若點P、Q出發的同時,點M從原點O以每秒3個單位長度的速度沿數軸向右勻速運動,求:出發幾秒后MP=MQ? ?組卷:674引用:4難度:0.5
?組卷:674引用:4難度:0.5


