2023年安徽省合肥市廬陽區壽春中學中考數學一模試卷

一、選擇題（本大題共10小題，每小題4分，滿分40分）

• 1．下列圖書館的標志中，是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：197引用：15難度：0.9

  解析

• 2．將拋物線y=3x²-2先向右平移3個單位長度，再向下平移2個單位長度得到的新拋物線解析式為（　　）

  A．y=3（x+3）2-4	B．y=3（x-3）2
  C．y=3（x-3）2-4	D．y=3（ x+3）2
  組卷：943引用：13難度：0.5

  解析

• 3．若雙曲線y=

  1

  -

  k

  x

  的圖象的一支位于第三象限，則k的取值范圍是（　　）

  A．k＜1

  B．k＞1

  C．0＜k＜1

  D．k≤1
  組卷：205引用：5難度：0.6

  解析

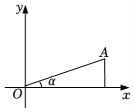• 4．如圖，在平面直角坐標系中，點A坐標為（3，1），則sinα的值為（　　）

  A． 1 3

  B． 10 10

  C． 10 3

  D． 3 10 10
  組卷：557引用：6難度：0.7

  解析

• 5．制作一塊3m×2m長方形廣告牌的成本是120元，在每平方米制作成本相同的情況下，若將此廣告牌的四邊都擴大為原來的3倍，那么擴大后長方形廣告牌的成本是（　　）

  A．360元

  B．1080元

  C．720元

  D．2160元
  組卷：396引用：3難度：0.7

  解析

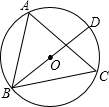• 6．如圖，△ABC內接于⊙O，BD是⊙O的直徑．若∠DBC=33°，則∠A等于（　　）

  A．33°

  B．57°

  C．67°

  D．66°
  組卷：1362引用：19難度：0.7

  解析

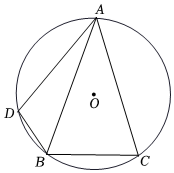• 7．如圖，⊙O是△ABC的外接圓，且AB=AC，∠BAC=36°，在

  ?

  AB

  上取點D（不與點A，B重合），連接BD，AD，則∠BAD+∠ABD的度數是（　　）

  A．60°

  B．62°

  C．72°

  D．73°
  組卷：2135引用：11難度：0.5

  解析

七、（本題滿分12分）

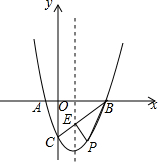• 22．如圖，拋物線y=ax²+bx-3過點A（-1，0），B（3，0），且與y軸交于點C，點E是拋物線對稱軸與直線BC的交點
  （1）求拋物線的解析式；
  （2）求證：BE=2CE；
  （3）若點P是第四象限內拋物線上的一動點，設點P的橫坐標為x,以點B、E、P為頂點的△BEP的面積為S，求S關于x的函數關系式，并求S的最大值．
  組卷：544引用：3難度：0.1

  解析

八、（本題滿分14分）

• 23．【問題提出】如圖1，AB為⊙O的一條弦，點C在弦AB所對的優弧上運動時，根據圓周角性質，我們知道∠ACB的度數不變．愛動腦筋的小芳猜想，如果平面內線段AB的長度已知，∠ACB的大小確定，那么點C是不是在某個確定的圓上運動呢？
  【問題探究】為了解決這個問題，小芳先從一個特殊的例子開始研究．如圖2，若AB=4，線段AB上方一點C滿足∠ACB=45°，為了畫出點C所在的圓，小芳以AB為底邊構造了一個Rt△AOB，再以點O為圓心，OA為半徑畫圓，則點C在⊙O上．后來小芳通過逆向思維及合情推理，得出一個一般性的結論．即：若線段AB的長度已知，∠ACB的大小確定，則點C一定在某一個確定的圓上，即定弦定角必定圓，我們把這樣的幾何模型稱之為“定弦定角”模型．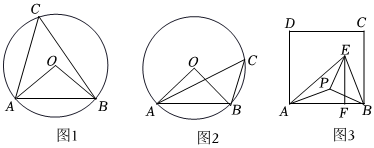
  
  【模型應用】
  （1）若AB=6，平面內一點C滿足∠ACB=60°，若點C所在圓的圓心為O，則∠AOB=

  ，劣弧AB的長為

  ．
  （2）如圖3，已知正方形ABCD以AB為腰向正方形內部作等腰△ABE，其中AB=AE，過點E作EF⊥AB于點F，若點P是△AEF的內心．
  ①求∠BPE的度數；
  ②連接CP，若正方形ABCD的邊長為4，求CP的最小值．
  組卷：547引用：3難度：0.5

  解析