當前位置：試卷中心 > 試卷詳情

2021-2022學年江蘇省南京師大蘇州實驗學校高一（上）期中數(shù)學試卷

發(fā)布：2024/10/7 14:0:2

一、單項選擇題（本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的）

1．復數(shù)
z
=
2
+
i
1
-
i
則在復平面內，z對應的點的坐標是（　　）
A．（1，0） B．（0，1） C．
（
1
2
，
3
2
）
D．
（
-
4
3
，-
5
3
）
組卷：54引用：2難度：0.8
解析
2．已知向量
a
=（1，3），
b
=（-6，m），若
a
與
b
垂直，則實數(shù)m=（　　）
A．-2 B．2 C．-8 D．8
組卷：136引用：2難度：0.8
解析
3．已知某圓錐的母線長為3，底面圓的半徑為2．則圓錐的表面積為（　　）
A．10π B．12π C．14π D．16π
組卷：26引用：2難度：0.6
解析
4．當復數(shù)z滿足|z-3+4i|=1時，則|z-2|的最大值是（　　）
A．
41
+1 B．
17
+1 C．
15
+1 D．
13
+1
組卷：163引用：3難度：0.8
解析
5．在△ABC中，已知a,b,c分別為角A，B，C的對邊且∠A=120°，若
S
△
ABC
=
3
3
2
且2sinB=3sinC，則△ABC的周長等于（　　）
A．
5
+
7
B．12 C．
10
+
7
D．
5
+
19
組卷：10引用：1難度：0.6
解析
6．已知O為△ABC所在平面內一點，若
（
OA
+
OB
）
?
AB
=
（
OB
+
OC
）
?
BC
=
0
，AB=4，AC=2，則
AO
?
BC
=（　　）
A．-8 B．8 C．-6 D．16
組卷：127引用：3難度：0.6
解析
7．《數(shù)書九章》是中國南宋時期杰出數(shù)學家秦九韶的著作，全書十八卷共八十一個問題，分為九類，每類九個問題，《數(shù)書九章》中記錄了秦九韶的許多創(chuàng)造性成就，其中在卷五“三斜求積”中提出了已知三角形三邊a,b,c求面積的公式，這與古希臘的海倫公式完成等價，其求法是：“以小斜冪并大斜冪減中斜冪，余半之，自乘于上，以小斜冪乘大斜冪減上，余四約之，為實，一為從隅，開平方得積．”若把以上這段文字寫成公式，即S=
1
4
[
c
2
a
2
-
（
c
2
+
a
2
-
b
2
2
）
2
]
，現(xiàn)有周長為10+2
7
的△ABC滿足sinA：sinB：sinC=2：3：
7
，則用以上給出的公式求得△ABC的面積為（　　）
A．
6
3
B．
4
7
C．
8
7
D．12
組卷：313引用：14難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本大題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟.

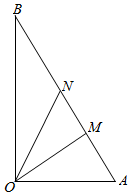21．如圖所示，某鎮(zhèn)有一塊空地△OAB，其中OA=3km,∠OAM=60°，∠AOB=90°．當?shù)卣媱潓⑦@塊空地改造成一個旅游景點，擬在中間挖一個人工湖△OMN，其中M，N都在邊AB上，且∠MON=30°，挖出的泥土堆放在△OAM地帶上形成假山，剩下的△OBN地帶開設兒童游樂場．為安全起見，需在△OAN的周圍安裝防護網．設∠AOM=θ．
（1）當
AM
=
3
2
km
時，求θ的值，并求此時防護網的總長度；
（2）若θ=15°，問此時人工湖用地△OMN的面積是堆假山用地△OAM的面積的多少倍？
（3）為節(jié)省投入資金，人工湖△OMN的面積要盡可能小，問如何設計施工方案，可使△OMN的面積最小？最小面積是多少？
組卷：238引用：8難度：0.4
解析
22．已知O為坐標原點，對于函數(shù)f（x）=asinx+bcosx,稱向量
OM
=（a,b）為函數(shù)f（x）的相伴特征向量，同時稱函數(shù)f（x）為向量
OM
的相伴函數(shù)．
（1）設函數(shù)
g
（
x
）
=
sin
（
x
+
5
π
6
）
-
sin
（
3
π
2
-
x
）
，試求g（x）的相伴特征向量
OM
；
（2）記向量
ON
=（1，
3
）的相伴函數(shù)為f（x），求當
f
（
x
）
=
8
5
且x∈（
-
π
3
，
π
6
）時，sinx的值；
（3）已知A（-2，3），B（2，6），
OT
=（
-
3
，1）為
h
（
x
）
=
msin
（
x
-
π
6
）
的相伴特征向量，
φ
（
x
）
=
h
（
x
2
-
π
3
）
，請問在y=φ（x）的圖象上是否存在一點P，使得
AP
⊥
BP
．若存在，求出P點坐標；若不存在，說明理由．
組卷：383引用：18難度：0.5
解析