2022-2023學(xué)年湖南省衡陽(yáng)八中高一（下）月考數(shù)學(xué)試卷（3月份）

一、單選題（本大題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的）

• 1．sin240°=（　　）

  A． - 3 2

  B．-1

  C． - 3 2 - 1

  D． - 3 2
  組卷：570引用：2難度：0.8

  解析

• 2．設(shè)a,b∈R，則“a+b＞2”是“a＞1且b＞1”的（　　）

  A．充分非必要條件	B．必要非充分條件
  C．充分必要條件	D．既非充分又非必要條件
  組卷：115引用：10難度：0.9

  解析

• 3．坐標(biāo)平面內(nèi)點(diǎn)P的坐標(biāo)為（sin5，cos5），則點(diǎn)P位于第（　　）象限．

  A．一

  B．二

  C．三

  D．四
  組卷：1073引用：7難度：0.8

  解析

• 4．已知點(diǎn)A（1，2），B（-2，6），則與

  AB

  方向相反的單位向量是（　　）

  A．（3，-4）

  B．（-3，-4）

  C． （ 3 5 ，- 4 5 ）

  D． （ - 3 5 ，- 4 5 ）
  組卷：179引用：4難度：0.8

  解析

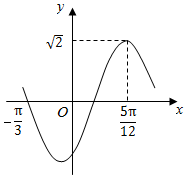• 5．函數(shù)f（x）=Asin（ωx+φ）（ω＞0，|φ|＜

  π

  2

  ）的部分圖象如圖所示，則φ=（　　）

  A． π 3

  B．- π 3

  C． π 6

  D．- π 6
  組卷：381引用：4難度：0.7

  解析

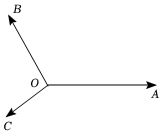• 6．如圖所示，平面內(nèi)有三個(gè)向量

  OA

  ，

  OB

  ，

  OC

  ，

  OA

  與

  OB

  的夾角為120°，

  OA

  與

  OC

  的夾角為150°，且

  |

  OA

  |

  =

  |

  OB

  |

  =

  1

  ，

  |

  OC

  |

  =

  3

  3

  ，若

  OB

  =

  λ

  OA

  +

  μ

  OC

  （λ，μ∈R），則λ+μ=（　　）

  A．1

  B．-1

  C．-4

  D．-5
  組卷：92引用：5難度：0.6

  解析

• 7．設(shè)函數(shù)

  f

  （

  x

  ）

  =

  2

  sin

  （

  ωx

  +

  φ

  ）

  -

  1

  （

  ω

  ＞

  0

  ，

  0

  ≤

  φ

  ≤

  π

  2

  ）

  的最小正周期為4π，且f（x）在[0，5π]內(nèi)恰有3個(gè)零點(diǎn)，則φ的取值范圍是（　　）

  A． [ 0 ， π 3 ] ∪ { 5 π 12 }

  B． [ 0 ， π 4 ] ∪ [ π 3 ， π 2 ]

  C． [ 0 ， π 6 ] ∪ { 5 π 12 }

  D． [ 0 ， π 6 ] ∪ [ π 3 ， π 2 ]
  組卷：946引用：13難度：0.5

  解析

四、解答題（本大題共6小題，共70分．解答應(yīng)寫出文字說(shuō)明，證明過(guò)程或演算步驟）

• 21．在△ABC中，內(nèi)角A，B，C所對(duì)的邊分別為a,b,c,且tanA=sinB．
  （1）證明：2ac=b²+c²-a²；
  （2）若

  BD

  =

  DC

  ，且AD=AB，求

  sin

  ∠

  BAC

  sin

  C

  ．
  組卷：90引用：4難度：0.5

  解析

• 22．設(shè)函數(shù)f（x）和g（x）的定義域分別為D₁和D₂，若對(duì)?x₀∈D₁，都存在n個(gè)不同的實(shí)數(shù)x₁，x₂，x₃，…，x_n∈D₂，使g（x_i）=f（x₀）（其中i=1，2，3，…，n,n∈N⁺），則稱g（x）為f（x）的“n重覆蓋函數(shù)”．
  （1）試判斷g（x）=2sin（2x-

  π

  3

  ）（0≤x≤2π）是否為f（x）=-（

  1

  2

  ）^|x|的“4重覆蓋函數(shù)”？并說(shuō)明理由．
  （2）已知函數(shù)g（x）=

  a x 2 + （ 2 a - 3 ） x + 1 ，- 2 ≤ x ≤ 1

  log 2 x , x ＞ 1

  為

  f

  （

  x

  ）

  =

  log

  2

  2

  x

  +

  2

  2

  x

  +

  1

  的“2重覆蓋函數(shù)”，求實(shí)數(shù)a的取值范圍
  組卷：51引用：3難度：0.6

  解析