當前位置：試卷中心 > 試卷詳情

2022-2023學年山東省青島市嶗山區九年級（下）開學數學試卷

發布：2024/12/29 9:30:2

一、選擇題（本大題共8小題，每小題3分，共24分）

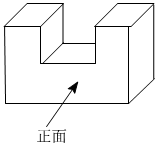1．如圖是一個零件的示意圖，它的俯視圖是（　　）
A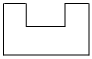． B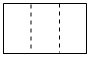． C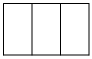． D．
組卷：625引用：12難度：0.9
解析
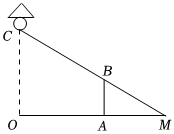2．如圖，路燈離地面距離OC=8m,若身高AB=1.6m的小明站在點A處，小明的影子AM的長為5米，則點A離點O的距離是（　　）
A．15m B．20m C．24m D．25m
組卷：29引用：2難度：0.5
解析
3．某機械廠七月份生產零件50萬個，第三季度生產零件196萬個．設該廠八、九月份平均每月的增長率為x,那么x滿足的方程是（　　）
A．50（1+x²）=196
B．50+50（1+x²）=196
C．50+50（1+x）+50（1+x）²=196
D．50+50（1+x）+50（1+2x）=196
組卷：3627引用：195難度：0.9
解析
4．已知反比例函數y=-
6
x
，下列結論中不正確的是（　　）
A．圖象必經過點（-3，2）
B．圖象位于第二、四象限
C．若x＜2，則y＜-3
D．當x＜0時，y隨x值的增大而增大
組卷：329引用：2難度：0.5
解析

5．要得到拋物線y=2（x-4）²-1，可以將拋物線y=2x²（　　）

A．向左平移4個單位長度，再向上平移1個單位長度

B．向左平移4個單位長度，再向下平移1個單位長度

C．向右平移4個單位長度，再向下平移1個單位長度

D．向右平移4個單位長度，再向上平移1個單位長度

組卷：1169引用：14難度：0.7

解析

6．下列形狀分別為兩個正方形、矩形、正三角形、圓的邊框，其中不一定是相似圖形的是（　　）
A． B．
C． D．
組卷：519引用：10難度：0.8
解析
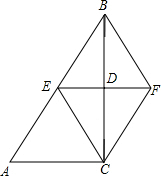7．如圖，在△ABC中，∠ACB=90°，BC的垂直平分線EF交BC于點D，交AB于點E，且BE=BF，添加一個條件，仍不能證明四邊形BECF為正方形的是（　　）
A．BC=AC B．BD=DF C．AC=BF D．CF⊥BF
組卷：1173引用：10難度：0.7
解析
8．已知拋物線y=ax²+3x+（a-2），a是常數且a＜0，下列選項中可能是它大致圖象的是（　　）
A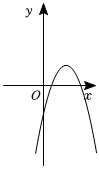． B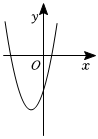． C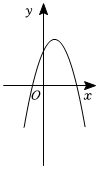． D．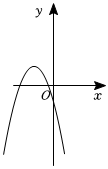
組卷：175引用：2難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本大題共9小題，共74分）

23．提出問題：如圖①，在四邊形ABCD中，P是AD邊上任意一點，△PBC與△ABC和△DBC的面積之間有什么關系？
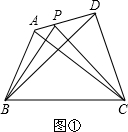
探究發現：為了解決這個問題，我們可以先從一些簡單的、特殊的情形入手：
（1）當AP=
1
2
AD時（如圖②）：

∵AP=
1
2
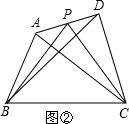
AD，△ABP和△ABD的高相等，
∴S_△ABP=
1
2
S_△ABD．
∵PD=AD-AP=
1
2
AD，△CDP和△CDA的高相等，
∴S_△CDP=
1
2
S_△CDA．
∴S_△PBC=S_{四邊形ABCD}-S_△ABP-S_△CDP
=S_{四邊形ABCD}-
1
2
S_△ABD-
1
2
S_△CDA
=S_{四邊形ABCD}-
1
2
（S_{四邊形ABCD}-S_△DBC）-
1
2
（S_{四邊形ABCD}-S_△ABC）
=
1
2
S_△DBC+
1
2
S_△ABC．
（2）當AP=
1
3
AD時，探求S_△PBC與S_△ABC和S_△DBC之間的關系，寫出求解過程；
（3）當AP=
1
6
AD時，S_△PBC與S_△ABC和S_△DBC之間的關系式為：

；
（4）一般地，當AP=
1
n
AD（n表示正整數）時，探求S_△PBC與S_△ABC和S_△DBC之間的關系，寫出求解過程；
問題解決：當AP=
m
n
AD（0≤
m
n
≤1）時，S_△PBC與S_△ABC和S_△DBC之間的關系式為：

．
組卷：7049引用：16難度：0.1
解析
24．如圖1，已知二次函數y=ax²+
3
2
x+c（a≠0）的圖象與y軸交于點A（0，4）．與x軸交于點B，C，點C坐標為（8，0），連接AB、AC．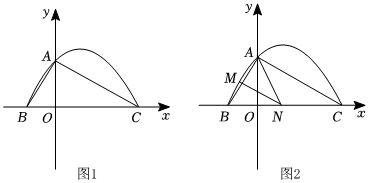

（1）請直接寫出二次函數y=ax²+
3
2
x+c（a≠0）的表達式；
（2）判斷△ABC的形狀，并說明理由；
（3）如圖2，若點N在線段BC上運動（不與點B，C重合），過點N作NM∥AC，交AB于點M，當△AMN面積最大時，求此時點N的坐標；
（4）若點N在x軸上運動，當以點A，N，C為頂點的三角形是等腰三角形時，請寫出此時點N的坐標．
組卷：562引用：3難度：0.2
解析