2021-2022學年浙江省溫州市永嘉縣上塘城西中學九年級（上）開學數學試卷

一、選擇題（本題有10小題，每小題4分，共40分，每小題只有一個選項是正確的，選擇正確才給分）

• 1．下列函數中，①y=2x；②y=2-x；③y=-

  2

  x

  ；④y=x²+6x+8．函數圖象經過第四象限的有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：94引用：3難度：0.6

  解析

• 2．從長度分別為1cm、3cm、5cm、6cm四條線段中隨機取出三條，則能夠組成三角形的概率為（　　）

  A． 1 4

  B． 1 3

  C． 1 2

  D． 3 4
  組卷：943引用：13難度：0.4

  解析

• 3．一個不透明的袋中有四張完全相同的卡片，把它們分別標上數字1、2、3、4．隨機抽取一張卡片，然后放回，再隨機抽取一張卡片，則兩次抽取的卡片上數字之積為偶數的概率是（　　）

  A． 1 4

  B． 1 2

  C． 3 4

  D． 5 6
  組卷：1552引用：18難度：0.7

  解析

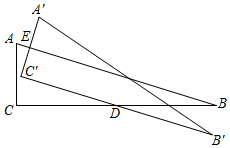• 4．如圖，在Rt△ABC中，∠C=90°，AC=7，BC=24，將它繞著BC中點D順時針旋轉一定角度后到△A'B'C'，恰好使B'C'∥AB，A'C'與邊AB交于點E，則A'E的長為（　　）

  A． 7 2

  B． 49 24

  C． 84 25

  D． 91 25
  組卷：53引用：2難度：0.6

  解析

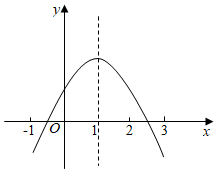• 5．二次函數y=ax²+bx+c（a≠0）的圖象如圖所示，現有以下結論：（1）b＞0；（2）abc＜0；（3）a-b+c＞0；（4）a+b+c＞0；（5）b²-4ac＞0，其中正確的結論有（　　）

  A．2個

  B．3個

  C．4個

  D．5個
  組卷：474引用：4難度：0.5

  解析

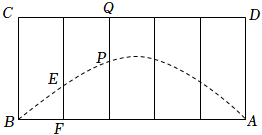• 6．我校門口道路的隔離欄通常會涂上醒目的顏色，呈拋物線形狀，如圖是一個長為2米，寬為1米的矩形隔離欄，中間被4根欄桿五等分，每根欄桿的下面一部分涂上醒目的藍色，顏色的分界處（點E，點P）以及點A，點B落上同一條拋物線上，若第1根欄桿涂色部分（EF）與第2根欄桿未涂色部分（PQ）長度相等，則EF的長度是（　　）

  A． 1 3 米

  B． 1 2 米

  C． 2 5 米

  D． 3 5 米
  組卷：44引用：1難度：0.4

  解析

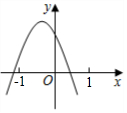• 7．已知二次函數y=ax²+bx+c的圖象如圖所示，則一次函數y=bx+c的圖象和反比例函數y=

  a

  +

  b

  +

  c

  x

  的圖象在同一坐標系中大致為（　　）

  A．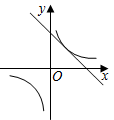

  B．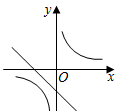

  C．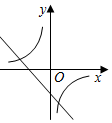

  D．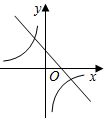
  組卷：1687引用：17難度：0.6

  解析

• 8．三孔橋橫截面的三個孔都呈拋物線形，兩小孔形狀、大小完全相同．當水面剛好淹沒小孔時，大孔水面寬度為10米，孔頂離水面1.5米；當水位下降，大孔水面寬度為14米時，單個小孔的水面寬度為4米若大孔水面寬度為20米，則單個小孔的水面寬度為（　　）

  A．4 3 米

  B．5 2 米

  C．2 13 米

  D．7米
  組卷：122引用：4難度：0.5

  解析

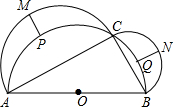• 9．如圖，C是以AB為直徑的半圓O上一點，連接AC，BC，分別以AC、BC為直徑作半圓，其中M，N分別是AC、BC為直徑作半圓弧的中點，

  ?

  AC

  ，

  ?

  BC

  的中點分別是P，Q．若MP+NQ=7，AC+BC=26，則AB的長是（　　）

  A．17

  B．18

  C．19

  D．20
  組卷：2756引用：9難度：0.5

  解析

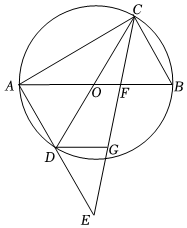• 10．如圖，在Rt△ABC中，∠ACB=90°，BC=

  5

  ．以AB為直徑作⊙O，作直徑CD，連結AD并延長至點E，使DE=AD，連結CE交AB于點F，DG∥AB交CE于點G．若AC=2EG，則直徑AB的長為（　　）

  A．3 2

  B． 19

  C．2 5

  D． 21
  組卷：282引用：3難度：0.5

  解析

二、填空題（本題共8小題，共40分，標明“?”符號題目在學校要求下選擇是否與附加題替換，替換后需寫附加題，不替換需寫原題）

• 11．一布袋里裝有4個紅球、5個黃球、6個黑球，這些球除顏色外其余都相同，那么從這個布袋里摸出一個黃球的概率為

  ．
  組卷：105引用：8難度：0.7

  解析

五、思維擴展（本題共8小題，共50分，分為選擇題，填空題與解答題，即為試卷第27-35題，難度較大）

• 34．在△ABC中，∠BAC=90°，AB=AC=2

  2

  ，D為BC的中點，E，F分別為AC，AD上任意一點，連接EF，將線段EF繞點E順時針旋轉90°得到線段EG，連接FG，AG．
  （1）如圖1，點E與點C重合，且GF的延長線過點B，若點P為FG的中點，連接PD，求PD的長；
  （2）如圖2，EF的延長線交AB于點M，點N在AC上，∠AGN=∠AEG且GN=MF，求證：AM+AF=

  2

  AE；
  （3）如圖3，F為線段AD上一動點，E為AC的中點，連接BE，H為直線BC上一動點，連接EH，將△BEH沿EH翻折至△ABC所在平面內，得到△B′EH，連接B′G，直接寫出線段B′G的長度的最小值．
  
  組卷：4906引用：10難度：0.3

  解析

• 35．如圖1，拋物線y=ax²+2x+c經過點A（-1，0）、C（0，3），并交x軸于另一點B，點P（x,y）在第一象限的拋物線上，AP交直線BC于點D．
  （1）求該拋物線的函數表達式；
  （2）當點P的坐標為（1，4）時，求四邊形BOCP的面積；
  （3）點Q在拋物線上，當

  PD

  AD

  的值最大且△APQ是直角三角形時，求點Q的橫坐標；
  （4）如圖2，作CG⊥CP，CG交x軸于點G（n,0），點H在射線CP上，且CH=CG，過GH的中點K作KI∥y軸，交拋物線于點I，連接IH，以IH為邊作出如圖所示正方形HIMN，當頂點M恰好落在y軸上時，請直接寫出點G的坐標．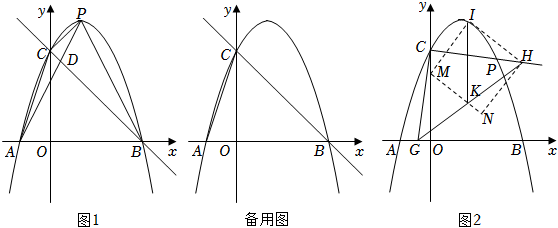
  
  組卷：1676引用：3難度：0.1

  解析