2022-2023學年江蘇省常州二十四中七年級（下）期中數(shù)學試卷

一、選擇題（每題2分，共16分）

• 1．下列各式由左邊到右邊的變形中，是因式分解的是（　　）

  A．a（x-y）=ax-ay	B．a2-b2=（a+b）（a-b）
  C．x2-4x+3=x（x-4）+3	D．a2+1=a（a+ 1 a ）
  組卷：2468引用：28難度：0.8

  解析

• 2．下列方程中，屬于二元一次方程的是（　　）

  A．5x-y=3z

  B．x2-y=3

  C． x + 1 y = 3

  D．3y+x=1
  組卷：194引用：5難度：0.8

  解析

• 3．周末李強和朋友到森林公園游玩，為測量園內湖岸A，B兩點之間的距離，如圖，李強在湖的一側選取了一點O，測得OA=20m,OB=8m,則A，B間的距離可能是（　　）

  A．10m

  B．22m

  C．30m

  D．32m
  組卷：294引用：7難度：0.6

  解析

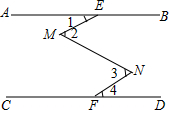• 4．如圖，AB∥CD，EMNF是直線AB、CD間的一條折線．若∠1=40°，∠2=60°，∠3=70°，則∠4的度數(shù)為（　　）

  A．55°

  B．50°

  C．40°

  D．30°
  組卷：659引用：3難度：0.7

  解析

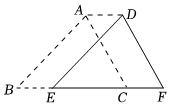• 5．如圖，△ABC向右平移2cm得到△DEF，如果四邊形ABFD的周長是20cm,那么△ABC的周長是（　　）

  A．14cm

  B．16cm

  C．18cm

  D．20cm
  組卷：663引用：5難度：0.7

  解析

• 6．如果在計算（x+m）（x-6）所得的結果中不含x的一次項，則常數(shù)m的值為（　　）

  A．m=0

  B．m=6

  C．m=-6

  D．m=1
  組卷：1236引用：4難度：0.7

  解析

• 7．如圖，點D，E分別是△ABC邊BC，AC上一點，BD=2CD，AE=CE，連接AD，BE交于點F，若△ABC的面積為18，則△BDF與△AEF的面積之差S_△BDF-S_△AEF等于（　　）

  A．3

  B． 18 5

  C． 9 2

  D．6
  組卷：2370引用：14難度：0.4

  解析

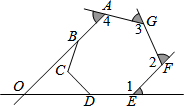• 8．如圖的七邊形ABCDEFG中，AB、ED的延長線相交于O點．若圖中∠1、∠2、∠3、∠4的外角的角度和為220°，則∠BOD的度數(shù)為何？（　　）

  A．40°

  B．45°

  C．50°

  D．60°
  組卷：5855引用：41難度：0.7

  解析

四、解答題（第22、23題各7分，24題8分，25題10分）

• 24．配方法是數(shù)學中非常重要的一種思想方法，它是指將一個式子或將一個式子的某一部分通過恒等變形化為完全平方式或幾個完全平方式的和的方法，這種方法常被用到代數(shù)式的變形中，并結合非負數(shù)的意義來解決問題．
  定義：若一個整數(shù)能表示成a²+b²（a,b為整數(shù)）的形式，則稱這個數(shù)為“完美數(shù)”．
  例如，5是“完美數(shù)”，理由：因為5=1²+2²，所以5是“完美數(shù)”．
  解決問題：
  （1）已知29是“完美數(shù)”，請將它寫成a²+b²（a,b為整數(shù)）的形式；
  （2）若x²-4x+5可配方成（x-m）²+n（m,n為常數(shù)），求mn的值；
  （3）已知S=x²+4y²+4x-12y+k（x,y是整數(shù)，k是常數(shù)），要使S為“完美數(shù)”，試求出k值．
  組卷：995引用：15難度：0.6

  解析

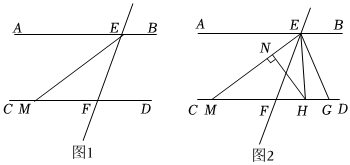
• 25．如圖1，已知兩條直線AB，CD被直線EF所截，分別交于點E，點F，EM平∠AEF交CD于點M，且∠FEM=∠FME．
  ?
  （1）判斷直線AB與直線CD是否平行，并說明理由；
  （2）如圖2，點G是射線MD上一動點（不與點M，F(xiàn)重合），EH平分∠FEG交CD于點H，過點H作HN⊥EM于點N，設∠EHN=α，∠EGF=β．
  ①當點G在點F的右側時，若α=30°，求β的度數(shù)；
  ②當點G在運動過程中，α和β之間有怎樣的數(shù)量關系？請寫出你的猜想，并加以證明．
  組卷：779引用：1難度：0.2

  解析