2022-2023學年江西省吉安市吉水二中高二（上）期末數學試卷

一、單選題（共40分）

• 1．直線l：

  3

  x-3y+1=0的傾斜角為（　　）

  A． π 3

  B． π 4

  C． π 6

  D． π 2
  組卷：308引用：6難度：0.8

  解析

• 2．命題“m=-2”是命題“直線2x+my-2m+4=0與直線mx+2y-m+2=0平行”的（　　）

  A．充要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：99引用：11難度：0.9

  解析

• 3．已知圓O₁的方程為（x-a）²+（y-b）²=4，圓O₂的方程為x²+（y-b+1）²=1，其中a,b∈R．那么這兩個圓的位置關系不可能為（　　）

  A．外離

  B．外切

  C．內含

  D．內切
  組卷：368引用：5難度：0.7

  解析

• 4．計算

  C

  3

  4

  +

  C

  3

  5

  +

  C

  3

  6

  +?+

  C

  3

  2015

  的值為（　　）

  A． C 4 2015

  B． C 3 2015

  C． C 4 2016 -1

  D． C 5 2015 -1
  組卷：372引用：1難度：0.8

  解析

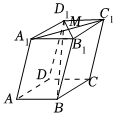• 5．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，M是A₁C₁與B₁D₁的交點，若

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，且

  MB

  =

  x

  a

  +

  y

  b

  +

  z

  c

  ，則x+y+z等于（　　）

  A．1

  B． - 1 2

  C．0

  D．-1
  組卷：69引用：4難度：0.7

  解析

• 6．已知F₁，F₂分別是雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右焦點，過點F₂且傾斜角為150°的直線交y軸于點A，交雙曲線的左支于點B，若

  AB

  +

  A

  F

  2

  =

  0

  ，則C的漸近線方程為（　　）

  A． y =± 3 3 x

  B． y =± 3 x

  C． y =± 2 2 x

  D． y =± 2 x
  組卷：86引用：2難度：0.6

  解析

• 7．已知拋物線C：y²=8x,點P為拋物線上任意一點，過點P向圓D：x²+y²-4x+3=0作切線，切點分別為A，B，則四邊形PADB的面積的最小值為（　　）

  A．1

  B．2

  C． 3

  D． 5
  組卷：93引用：3難度：0.5

  解析

四、解答題（共70分）

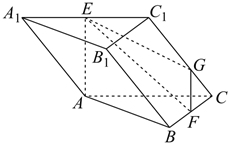• 21．如圖，三棱柱ABC-A₁B₁C₁的底面ABC是正三角形，側面ACC₁A₁是菱形，平面ACC₁A₁⊥平面ABC，E，F分別是棱A₁C₁，BC的中點．
  （1）證明：EF∥平面ABB₁A₁；
  （2）若

  AC

  =

  2

  ，

  ∠

  AC

  C

  1

  =

  60

  °

  ，

  C

  1

  G

  =

  2

  GC

  ，求直線B₁C₁與平面EFG所成角的正弦值．
  組卷：237引用：6難度：0.5

  解析

• 22．某同學在探究直線與橢圓的位置關系時發現橢圓的一個重要性質：橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  在任意一點M（x₀，y₀）處的切線方程為

  x

  x

  0

  a

  2

  +

  y

  y

  0

  b

  2

  =

  1

  ．現給定橢圓

  C

  ：

  x

  2

  4

  +

  y

  2

  3

  =

  1

  ，過C的右焦點F的直線l交橢圓C于P，Q兩點，過P，Q分別作C的兩條切線，兩切線相交于點G．
  （1）求點G的軌跡方程；
  （2）若過點F且與直線l垂直的直線（斜率存在且不為零）交橢圓C于M，N兩點，證明：

  1

  |

  PQ

  |

  +

  1

  |

  MN

  |

  為定值．
  組卷：67引用：3難度：0.4

  解析